I find it very interesting that even with the exponential growth in knowledge that we have witnessed from ancient times through the industrial age to the digital age, there still remains so much that is simply unknown to us. I have no doubt that the human spirit will in time conquer each and every question that it poses to itself. The following is a list of unsolved problems in various fields of scientific and philosophical inquiry. Aside from the solutions being interesting in themselves and offering the opportunity of contributing to our collective history, some of these problems even offer monetary incentives for proven solutions. So go ahead and tackle one!
We know very little, and yet it is astonishing that we know so much, and still more astonishing that so little knowledge can give us so much power.
– Bertrand Russell
Unsolved Problems in Artificial Intelligence
In the field of artificial intelligence, the most difficult problems are informally known as AI-complete or AI-hard, implying that the difficulty of these computational problems is equivalent to that of solving the central artificial intelligence problem—making computers as intelligent as people, or strong AI.[1] To call a problem AI-complete reflects an attitude that it would not be solved by a simple specific algorithm.
AI-complete problems are hypothesised to include computer vision, natural language understanding, and dealing with unexpected circumstances while solving any real world problem.[2]
Currently, AI-complete problems cannot be solved with modern computer technology alone, but would also require human computation. This property can be useful, for instance to test for the presence of humans as with CAPTCHAs, and for computer security to circumvent brute-force attacks.[3][4]
History
The term was coined by Fanya Montalvo by analogy with NP-complete and NP-hard in complexity theory, which formally describes the most famous class of difficult problems.[5] Early uses of the term are in Erik Mueller’s 1987 Ph.D. dissertation[6] and in Eric Raymond‘s 1991 Jargon File.[7]
AI-complete problems
AI-complete problems are hypothesised to include:
- Computer vision (and subproblems such as object recognition)
- Natural language understanding (and subproblems such as text mining, machine translation, and word sense disambiguation)
- Dealing with unexpected circumstances while solving any real world problem, whether it’s navigation or planning or even the kind of reasoning done by expert systems.
Machine translation
To translate accurately, a machine must be able to understand the text. It must be able to follow the author’s argument, so it must have some ability to reason. It must have extensive world knowledge so that it knows what is being discussed — it must at least be familiar with all the same commonsense facts that the average human translator knows. Some of this knowledge is in the form of facts that can be explicitly represented, but some knowledge is unconscious and closely tied to the human body: for example, the machine may need to understand how an ocean makes one feel to accurately translate a specific metaphor in the text. It must also model the authors’ goals, intentions, and emotional states to accurately reproduce them in a new language. In short, the machine is required to have wide variety of human intellectual skills, including reason, commonsense knowledge and the intuitions that underlie motion and manipulation, perception, and social intelligence.Machine translation, therefore, is believed to be AI-complete: it may require strong AI to be done as well as humans can do it.
Software brittleness
Current AI systems can solve very simple restricted versions of AI-complete problems, but never in their full generality. When AI researchers attempt to “scale up” their systems to handle more complicated, real world situations, the programs tend to become excessively brittle without commonsense knowledge or a rudimentary understanding of the situation: they fail as unexpected circumstances outside of its original problem context begin to appear. When human beings are dealing with new situations in the world, they are helped immensely by the fact that they know what to expect: they know what all things around them are, why they are there, what they are likely to do and so on. They can recognize unusual situations and adjust accordingly. A machine without strong AI has no other skills to fall back on.[8]
Formalization
Computational complexity theory deals with the relative computational difficulty of computable functions. By definition it does not cover problems whose solution is unknown or has not been characterised formally. Since many AI problems have no formalisation yet, conventional complexity theory does not allow the definition of AI-completeness.
To address this problem, a complexity theory for AI has been proposed.[9] It is based on a model of computation that splits the computational burden between a computer and a human: one part is solved by computer and the other part solved by human. This is formalised by a human-assisted Turing machine. The formalisation defines algorithm complexity, problem complexity and reducibility which in turn allows equivalence classes to be defined.
The complexity of executing an algorithm with a human-assisted Turing machine is given by a pair  , where the first element represents the complexity of the human’s part and the second element is the complexity of the machine’s part.
, where the first element represents the complexity of the human’s part and the second element is the complexity of the machine’s part.
Results
The complexity of solving the following problems with a human-assisted Turing machine is:[9]
- Optical character recognition for printed text:
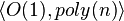
- Turing test:
- for an
 -sentence conversation where the oracle remembers the conversation history (persistent oracle):
-sentence conversation where the oracle remembers the conversation history (persistent oracle): 
- for an
 -sentence conversation where the conversation history must be retransmitted:
-sentence conversation where the conversation history must be retransmitted: 
- for an
 -sentence conversation where the conversation history must be retransmitted and the person takes linear time to read the query:
-sentence conversation where the conversation history must be retransmitted and the person takes linear time to read the query: 
- for an
- ESP game:

- Image labelling (based on the Arthur–Merlin protocol):

- Image classification: human only:
 , and with less reliance on the human:
, and with less reliance on the human: 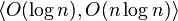 .
.
See also
References
- Jump up^ Shapiro, Stuart C. (1992). Artificial Intelligence In Stuart C. Shapiro (Ed.), Encyclopedia of Artificial Intelligence (Second Edition, pp. 54–57). New York: John Wiley. (Section 4 is on “AI-Complete Tasks”.)
- Jump up^ Roman V. Yampolskiy. Turing Test as a Defining Feature of AI-Completeness . In Artificial Intelligence, Evolutionary Computation and Metaheuristics (AIECM) –In the footsteps of Alan Turing. Xin-She Yang (Ed.). pp. 3-17. (Chapter 1). Springer, London. 2013. http://cecs.louisville.edu/ry/TuringTestasaDefiningFeature04270003.pdf
- Jump up^ Luis von Ahn, Manuel Blum, Nicholas Hopper, and John Langford. CAPTCHA: Using Hard AI Problems for Security. In Proceedings of Eurocrypt, Vol. 2656 (2003), pp. 294-311.
- Jump up^ Bergmair, Richard (January 7, 2006). “Natural Language Steganography and an “AI-complete” Security Primitive”. CiteSeerX: 10.1.1.105.129. (unpublished?)
- Jump up^ Mallery, John C. (1988), “Thinking About Foreign Policy: Finding an Appropriate Role for Artificially Intelligent Computers”, The 1988 Annual Meeting of the International Studies Association., St. Louis, MO.
- Jump up^ Mueller, Erik T. (1987, March). Daydreaming and Computation (Technical Report CSD-870017) Ph.D. dissertation, University of California, Los Angeles. (“Daydreaming is but one more AI-complete problem: if we could solve any one artificial intelligence problem, we could solve all the others”, p. 302)
- Jump up^ Raymond, Eric S. (1991, March 22). Jargon File Version 2.8.1 (Definition of “AI-complete” first added to jargon file.)
- Jump up^ Lenat, Douglas; Guha, R. V. (1989), Building Large Knowledge-Based Systems, Addison-Wesley, pp. 1–5
- ^ Jump up to:a b Dafna Shahaf and Eyal Amir (2007) Towards a theory of AI completeness. Commonsense 2007, 8th International Symposium on Logical Formalizations of Commonsense Reasoning.
Unsolved Problems in Biology
| Adaptation | At present there is no theoretical model for how adaptation occurs that is close to being complete. Mathematical models of evolution (e.g. within population genetics) describe how the process of natural selection influences the frequency of already-existing gene variants based on their relative fitnesses. Only a small amount of theory treats the problem of modelling the generation of new variants through mutation, in terms of either the fitnesses or phenotypic forms they confer. |
| Alkaloids | The function of these substances in living organisms which produce them is not known[1] |
| Arthropod head problem | A long-standing zoological dispute concerning the segmental composition of the heads of the various arthropod groups, and how they are evolutionarily related to each other. |
| Basking shark | Only the right ovary in this fish appears to function, the reason is unknown. |
| Biological aging | There are a number of hypotheses why senescence occurs including those that it is programmed by gene expression changes and that it is the accumulative damage of biological processes. |
| Blue Whale | There is not much data on the sexuality of the biggest animal ever.[2] |
| Botany/Plants | What is the exact evolutionary history of flowers and their blossoms? |
| Butterfly migration | How do the descendants of Monarch butterfly all over Canada and the US eventually, after migrating for several generations, manage to return to a few relatively small overwintering spots? |
| Cambrian explosion | What is the cause of the apparent rapid diversification of multicellular animal life around the beginning of the Cambrian, resulting in the emergence of almost all modern animal phyla? |
| Consciousness | What is the brain basis of subjective experience, cognition, wakefulness, alertness, arousal, and attention? Is there a “hard problem of consciousness“? If so, how is it solved? What, if any, is the function of consciousness?[3][4] |
| Evolution of sex | What selective advantages drove the development of sexual reproduction, and how did it develop?[5] |
| Extraterrestrial life | Might life which does not originate from planet Earth also have developed on other planets? Might this life be intelligent? |
| Gall wasp | It is largely unknown how these insects induce gall formation in plants; chemical, mechanical, and viral triggers have been discussed. |
| Glycogen body | The function of this structure is not known. |
| Golgi apparatus | In cell theory, what is the exact transport mechanism by which proteins travel through the Golgi apparatus? |
| Hammerhead shark | The reason for their distinctive and unusual head structure is not known. |
| Homing (biology) | A satisfactory explanation for the neurobiological mechanisms that allow Homing, has yet to be found. |
| Korarchaeota | Their metabolic processes are so far unclear. |
| Latitudinal diversity gradient | Why does biodiversity increase when going from the poles towards the equator? |
| Loricifera | There are at least 100 species of this phylum that are yet to be described, but none of them is known to be present in the fossil record. |
| Origin of life | Exactly how and when did life on Earth originate? Which, if any, of the many hypotheses is correct? |
| Paradox of the plankton | The high diversity of phytoplankton seems to violate the competitive exclusion principle. |
References
- Jump up^ Aniszewski, p. 142
- Jump up^ Articleworld.org Blue Whale
- Jump up^ Sejnowski, Terrence J.; Hemmen, J. L. van (2006). 23 problems in systems neuroscience (PDF). Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-514822-3.
- Jump up^ Tononi, G; Koch, C. (2015). “Consciousness: Here, there and everywhere?” (PDF). Philosophical Transactions of the Royal Society London B.
- Jump up^ Thomas N. Sherratt, David M. Wilkinson. Big questions in ecology and evolution. Oxford University Press US, 2009. ISBN 978-0-19-954861-3
Unsolved Problems in Chemistry
Unsolved problems in chemistry tend to be questions of the kind “Can we make X chemical compound?”, “Can we analyse it?”, “Can we purify it?” and are commonly solved rather quickly, but may just as well require considerable efforts to be solved. However, there are also some questions with deeper implications. This article tends to deal with the areas that are the center of new scientific research in chemistry. Problems in chemistry are considered unsolved when an expert in the field considers it unsolved or when several experts in the field disagree about a solution to a problem.
Physical chemistry problems
- What are the electronic structures of high-temperature superconductors at various points on their phase diagrams?[1]
- Can the transition temperature of high-temperature superconductors be brought up to room temperature?[1]
- Is Feynmanium the last chemical element that can physically exist? That is, what are the chemical consequences of having an element with an atomic number above 137, whose 1s electrons must travel faster than the speed of light?[1][2]
- How can electromagnetic energy (photons) be efficiently converted to chemical energy? For instance, can water be efficiently split to hydrogen and oxygen usingsolar energy?[3][4]
Organic chemistry problems
- Is an abiologic origin of chirality as is found in (2R)-2,3-dihydroxypropanal (D-glyceraldehyde), and also in amino acids, sugars, etc., possible?[5]
- Why are accelerated kinetics observed for some organic reactions at the water-organic interface?[6][non-primary source needed][citation needed]
- What is the origin of the energy barrier to bond rotation (e.g., in ethane), simple steric hindrance, hyperconjugation, or another explanation?[citation needed]
- What is the origin of the alpha effect, that is, that nucleophiles with an electronegative atom with lone pairs adjacent to the nucleophilic center are particularly reactive?[citation needed]
- What is the nature of strong gold-chalcogens in thiols and other organochalcogens (i.e., sulfur and higher chalcogen-containing organic compounds)?[7][self-published source?][better source needed]
In addition to these, it is noteworthy that many mechanisms proposed for catalytic processes are poorly understood[which?] and often fail to explain all relevant phenomena.[citation needed]
Biochemistry problems
- Enzyme kinetics: Why do some enzymes exhibit faster-than-diffusion kinetics?[8]
- Protein folding problem: Is it possible to predict the secondary, tertiary and quaternary structure of a polypeptide sequence based solely on the sequence and environmental information? Inverse protein-folding problem: Is it possible to design a polypeptide sequence which will adopt a given structure under certain environmental conditions?[5][9] This has been achieved for several small globular proteins in recent years.[10]
- RNA folding problem: Is it possible to accurately predict the secondary, tertiary and quaternary structure of a polyribonucleic acid sequence based on its sequence and environment?
- What are the chemical origins of life? How did non-living chemical compounds generate self-replicating, complex life forms?
- Protein design: Is it possible to design highly active enzymes de novo for any desired reaction?[11]
- Biosynthesis: Can desired molecules, natural products or otherwise, be produced in high yield through biosynthetic pathway manipulation?[12]
References
- ^ Jump up to:a b c The Future of Post-Human Chemistry: A Preface to a New Theory of Substances …, de Peter Baofu, page 285
- Jump up^ The problem may actually occur at approximately Element 173, given the finite extension of nuclear-charge distribution.[citation needed] See the article on Extension of the periodic table beyond the seventh period, and the article section Relativistic effects of Atomic orbital.
- Jump up^ Duffie, John A. (August 2006). Solar Engineering of Thermal Processes. Wiley-Interscience. p. 928. ISBN 978-0-471-69867-8.
- Jump up^ Brabec, Christoph; Vladimir Dyakonov; Jürgen Parisi; Niyazi Serdar Sarıçiftçi (March 2006). Organic Photovoltaics: Concepts and Realization. Springer. p. 300. ISBN 978-3-540-00405-9.
- ^ Jump up to:a b “So much more to know”. Science 309 (5731): 78–102. July 2005. doi:10.1126/science.309.5731.78b. PMID 15994524.
- Jump up^ S. Narayan, J. Muldoon, M.G. Finn, V.V. Fokin, H.C. Kolb, K.B. Sharpless,2005, “On Water: Unique Reactivity of Organic Compounds in Aqueous Suspension,” Angew. Chem. Int. Ed. 21:3157, see [onlinelibrary.wiley.com/doi/10.1002/anie.200462883/full]. accessed 15 December 2015.
- Jump up^ Fredrik von Kieseritzky, 2013, “What is the true nature of gold-sulfur bonds?”, see [1], accessed 15 December 2014.
- Jump up^ Hsieh M, Brenowitz M (August 1997). “Comparison of the DNA association kinetics of the Lac repressor tetramer, its dimeric mutant LacIadi, and the native dimeric Gal repressor”. J. Biol. Chem. 272 (35): 22092–6. doi:10.1074/jbc.272.35.22092. PMID 9268351.
- Jump up^ King, Jonathan (2007). “MIT OpenCourseWare – 7.88J / 5.48J / 7.24J / 10.543J Protein Folding Problem, Fall 2007 Lecture Notes – 1”. MIT OpenCourseWare. RetrievedJune 22, 2013.
- Jump up^ Dill KA; et al. (June 2008). “The Protein Folding Problem”. Annu Rev Biophys 37: 289–316. doi:10.1146/annurev.biophys.37.092707.153558. PMID 9268351.
- Jump up^ http://depts.washington.edu/bakerpg/drupal/node/465
- Jump up^ http://www.nature.com/nature/journal/v488/n7411/full/nature11478.html
External links
- “First 25 of 125 big questions that face scientific inquiry over the next quarter-century”. Science 309 (125th Anniversary). 1 July 2005.
- Unsolved Problems in Nanotechnology: Chemical Processing by Self-Assembly – Matthew Tirrell – Departments of Chemical Engineering and Materials, Materials Research Laboratory, California NanoSystems Institute, University of California, Santa Barbara
Unsolved Problems in Computer Science
This article is a list of unsolved problems in computer science. A problem in computer science is considered unsolved when an expert in the field (i.e, a computer scientist) considers it unsolved or when several experts in the field disagree about a solution to a problem.
Computational complexity
- P versus NP problem (often written as “P = NP,” which is technically not correct for the problem or those below)
- NC = P problem
- NP = co-NP problem
- P = BPP problem
- P = PSPACE problem
- L = NL problem
- L = P problem
- L = RL problem
- What is the relationship between BQP and NP?
- Unique games conjecture
- Is the exponential time hypothesis true?
- Do one-way functions exist?
- Is public-key cryptography possible?
Algorithms
- What is the fastest algorithm for multiplication of two n-digit numbers?
- What is the fastest algorithm for matrix multiplication?
- Can integer factorization be done in polynomial time on a classical computer?
- Can the discrete logarithm be computed in polynomial time on a classical computer?
- Can the graph isomorphism problem be solved in polynomial time?
- Can parity games be solved in polynomial time?
- Can the rotation distance between two binary trees be computed in polynomial time?
- Does linear programming admit a strongly polynomial-time algorithm? This is problem #9 in Smale’s list of problems.
- What is the lower bound on the complexity of fast Fourier transform algorithms? Can they be faster than Θ (N log N)?
- Dynamic optimality conjecture for splay trees
- K-server problem
- Can X + Y sorting be done in strictly less than O(n2 log n) time?
- Is there a bounded-time algorithm for Envy-free cake-cutting?
Programming language theory
Other problems
External links
- Major unsolved problems in theoretical computer science on StackExchange.
- Open problems around exact algorithms by Gerhard J. Woeginger, Discrete Applied Mathematics 156 (2008) 397–405.
- Challenges for Theoretical Computer Science (Broken link)
- The Open Problems Project – open problems in computational geometry and related fields.
- The RTA list of open problems – open problems in rewriting.
- The TLCA List of Open Problems – open problems in area typed lambda calculus.
Unsolved Problems in Economics
This is a list of some of the major unsolved problems, puzzles, or questions in neoclassical economics. Some of these are theoretical in origin and some of them concern the inability of orthodox economic theory to explain an empirical observation.
Behavioral economics
- Revealed preference: Does Revealed Preference theory truly reveal consumer preference when the consumer is able to afford all of the available options? For example, if a consumer is confronted with three goods and they can afford to purchase all three (A, B, and C) and they choose to first purchase A, then C, and then B – does this suggest that the consumer preference for the goods is A > C > B? The debate rests on the fact that since the consumer can afford all three goods and does not need to make a preferential decision, does the order of consumption reflect any preference?[1]
- Tâtonnement: The act of tâtonnement plays a key role in the formulation of general equilibrium theory. The claim is that if an initial contract does not lead to an equilibrium, it is ended and new contracts are formulated. If the initial contract is not called off, it will likely lead to a different set of prices, depending on the degree of error in the original process. The question is whether successive re-contracting continues with the parties forgetting the previously planned positions taken or whether the parties engage in a form of tâtonnement to achieve optimality.[1] See also Hill climbing and Walrasian auction.
- Unified Models of Human Biases: Neoclassical economics has concentrated on the development of models that reflect an idealized economic agent, sometimes referred to as Homo economicus, as a way of studying economics. In the period spanning the 1970s to the 1990s, research began to emerge that suggested that people were subject to cognitive biases such as the framing effect, loss aversion, the gambler’s fallacy, confirmation bias, and many others. Further, these effects could produce anomalies such as herd behavior or momentum investing inconsistent with economic models that did not incorporate human psychological limitations.[2] While some models have begun to include bounded rationality and risk aversion, such as Prospect Theory, there still remains to be seen a unified model that can make useful predictions that incorporates the entirety of cognitive biases and rational limitations in most humans.[3] Further, there even exists debate as to whether it is necessary to incorporate such psychological limitations into economic models. While some economists insist they are necessary to fully appreciate the complexity of the market, others still contend that a model that incorporates human biases is either unrealistic or question its usefulness arguing that a model that doesn’t approximate agents as being perfectly rational, with the possibility of minimal exceptions, is unlikely to be successful.[3][4]
Financial economics
- Equity premium puzzle: The equity premium puzzle is thought to be one of the most important outstanding questions in neoclassical economics.[5] It is founded on the basis that over the last one hundred years or so the average real return to stocks in the US has been substantially higher than that of bonds. The puzzle lies in the explaining the causes behind this equity premium. While there are a number of different theories regarding the puzzle, there still exists no definitive agreement on its cause.[6]
- Dividend puzzle: The dividend puzzle is the empirically observed phenomenon that companies that pay dividends tend to be rewarded by investors with highervaluations. At present, there is no explanation widely accepted by economists.[7][8][9] The Modigliani-Miller theorem suggests that the puzzle can (only) be explained by some combination of taxes, bankruptcy costs, market inefficiency (including that due to investor psychology), and asymmetric information.
- Improved Black–Scholes and Binomial Options Pricing models: The Black–Scholes model and the more general binomial options pricing models are a collection of equations that seek to model and price equity and call options. While the models are widely used, they have many significant limitations.[10] Chief among them are the model’s inability to account for historical market movements[11] and their frequent overpricing of options, with the overpricing increasing with the time to maturity.[12] The development of a model that can properly account for the pricing of call options on an asset with stochastic volatility is considered an open problem in financial economics.[12]
- Problems with the American option: Is there a closed form for American put options? Is there a forward partial differential equation for the American Option in a local volatility model?
International economics
- Home bias in trade puzzle: The home bias in trade puzzle is an empirical observation that even when factors such as economic size of trading partners and the distance between them are considered, trade between regions within a given country is substantially greater than trade between regions in different countries, even when there are no substantial legal barriers. There is currently no framework to explain this observation.[13][14]
- Equity home bias puzzle: This puzzle concerns the observation that individuals and institutions in many countries only hold modest amounts of foreign equity, despite the ability for vast diversification of their portfolios in the global economy.[13] While some explanations do exist, such as that local individuals and firms have greater access to information about local firms and economic conditions, these explanations are not accepted by the majority of economists and have been mostly refuted.[15]
- Backus-Kehoe-Kydland puzzle: The Backus-Kehoe-Kydland consumption correlation puzzle is the empirical observation that consumption is much less correlated across countries than output.[13] Standard economic theory suggests that country-specific output risks should be collective and domestic consumption growth should not depend strongly on country-specific income shocks. Thus, we should not see the observation that consumption is much less correlated across countries than output; and yet we do.[16][17]
- Feldstein-Horioka puzzle: The Feldstein-Horioka puzzle originates from an article in the 1980s that found that among OECD countries, averages of long-term national savings rates are highly correlated with similar averages of domestic investment rates. Standard economic theory suggests that in relatively open international financial markets, the savings of any country would flow to countries with the most productive investment opportunities; hence, saving rates and domestic investment rates would be uncorrelated, contrary to the empirical evidence suggested by Martin Feldstein and Charles Horioka. While numerous articles regarding the puzzle have been published, none of the explanations put forth have adequate empirical support.[13]
- PPP Puzzle: The PPP puzzle, considered one of the two real exchange rate puzzles, concerns the observation that real exchange rates are both more volatileand more persistent than most models would suggest. The only clear way to understand this volatility would be to assign substantial roles to monetary and financial shocks. However, if shocks play such a large role the challenge becomes finding what source, if one even exists, of nominal rigidity that could be so persistent to explain the long-term prolonged nature of real exchange rate deviations.[13]
- The Exchange Rate Disconnect Puzzle: The exchange rate disconnect puzzle, also one of the so-called real exchange rate puzzles, concerns the weak short-term feedback link between exchange rates and the rest of the economy. In most economies, the exchange rate is the most important relative price, so it is surprising, and thus far unexplained entirely, that the correlations are not stronger.[13]
References
- ^ Jump up to:a b Oskar Morgenstern (1972). “Thirteen critical points in contemporary economic theory”. Journal of Economic Literature 10: 1163–1189. JSTOR 2721542.
- Jump up^ “Foundations of Behavioral and Experimental Economics: Daniel Kahneman and Vernon Smith” (PDF) (Press release). The Royal Swedish Academy of Sciences. 17 December 2002.
- ^ Jump up to:a b Machina, Mark (1987). “Choice under Uncertainty: Problems Solved and Unsolved” (PDF). Journal of Economic Perspectives 1 (1): 121–154. doi:10.1257/jep.1.1.121.
- Jump up^ Krugman, Paul (2 September 2009), “How Did Economists Get It So Wrong?”, The New York Times
- Jump up^ “Has Barro solved the equity premium puzzle?”. New Economist weblog. 2005-09-29.
- Jump up^ Narayana R. Kocherlakota (March 1996). “The Equity Premium: It’s Still a Puzzle” (PDF). Journal of Economic Literature 34: 42–71.
- Jump up^ Borges, Maria Rosa (July 2008), Is The Dividend Puzzle Solved ? (PDF)
- Jump up^ Prast, Henriette (March 2004), Investor psychology: a behavioral explanation of six finance puzzles (PDF)
- Jump up^ Bernheim, B. Douglas (1991). “Tax Policy and the Dividend Puzzle”. RAND Journal of Economics 22 (4): 455–476. doi:10.2307/2600982.
- Jump up^ http://www.wilmott.com/blogs/paul/index.cfm/2008/4/29/Science-in-Finance-IX-In-defence-of-Black-Scholes-and-Merton
- Jump up^ Baggett, L. Scott; Thompson, James; Williams, Edward; Wojciechowski, William (October 2006). “Nobels for nonsense”. Journal of Post Keynesian Economics 29 (1): 3–18.doi:10.2753/pke0160-3477290101.
- ^ Jump up to:a b Hull, John; White, Alan (June 1987). “The Pricing of Options on Assets with Stochastic Volatilities”. Journal of Finance 42 (2): 281–300. doi:10.1111/j.1540-6261.1987.tb02568.x.
- ^ Jump up to:a b c d e f Obstfeld, Maurice; Rogoff, Kenneth (2000), “The Six Major Puzzles in International Macroeconomics: Is There a Common Cause?”, in Bernanke, Ben; Rogoff, Kenneth, NBER Macroeconomics Annual 2000 15, The MIT Press, pp. 339–390, ISBN 0-262-02503-5
- Jump up^ Edmond, Chris, Note 8a from course 316–632 “International Monetary Economics” (PDF) (Handout)
- Jump up^ Van Nieuwerburgh, Stijn; Veldkamp, Laura (July 2005). “Information Immobility and the Home Bias Puzzle”. NYU Working Paper. FIN-04-026. ssrn 1294476.
- Jump up^ Backus, David K.; Kehoe, Patrick J.; Kydland, Finn E. (1992), “International Real Business Cycles”, Journal of Political Economy 100: 745–775, doi:10.1086/261838
- Jump up^ Backus, David K.; Kehoe, Patrick J.; Kydland, Finn E. (1995), “International Business Cycles: Theory and Evidence”, in Cooley, Tom, Frontiers of Business Cycle Research,Princeton University Press, ISBN 0-691-04323-X
Further reading
- Oskar Morgenstern (1972). “Thirteen critical points in contemporary economic theory”. Journal of Economic Literature 10: 1163–1189. JSTOR 2721542.
- Alessandro Innocenti (1995). “Oskar Morgenstern and the Heterodox Potentialities of the Application of Game Theory to Economics”. Journal of the History of Economic Thought (Cambridge University Press) 17: 205–227. doi:10.1017/S1053837200002601.
- Bernstein, Steven; Ned Lebow, Richard; Gross Stein, Janice; Weber, Steven (2000). “God Gave Physics the Easy Problems:”. European Journal of International Relations 6 (1): 43–76. doi:10.1177/1354066100006001003.
- Peter J. Boettke (Winter 1998). “Formalism and contemporary economics: A reply to Hausman, Heilbroner, and Mayer”. Critical Review 12 (1&2): 173–186.doi:10.1080/08913819808443492.
- DeLong, J. Bradford; Konstantin Magin (2009). “The U.S. Equity Return Premium: Past, Present, and Future”. Journal of Economic Perspectives (American Economic Association) 23 (1): 193–208. doi:10.1257/jep.23.1.193.
Unsolved Problems in Geoscience
This article discusses currently unsolved problems in geoscience.
The early Earth and the solar system
- How did Earth and other planets form? Were planets formed in situ? Or are orbital changes relatively frequent? What determined the different deep layering of the solar planets?[1]
- Was there ever a collision of the Earth with another planet Theia, giving birth to our satellite?[2] There is compelling evidence, such as measures of a shorter duration of the Earth’s rotation and lunar month in the past, pointing to a Moon much closer to Earth during the early stages of the Solar System.[3]
- What is the long-term heat balance of Earth? How did its internal temperature decay since it formed by accretion of chondrites? How abundant are radiogenic elements in the interior? Did a “faint young Sun” ever warm a “snowball Earth“? [4][5]
- What made plate tectonics a dominant process only on Earth?[6] How did the planet cool down before plate tectonics?[7] Was the Earth’s crust formed during the early stages of its evolution or is it the result of a gradual distillation of the mantle that continues today along with crustal recycling? Is the crust still growing or does its recycling compensate for crust formation at mid-ocean ridges and other volcanic areas?
Topography and environment
- Can the now widely available topographic data be used to derive past tectonic and climatic conditions (in the multi-million year scale)? Do we know enough about the erosion and transport processes? Does the stocasticity of meteorological and tectonic events reflect in the landscape? How much has life contributed to shape the Earth’s surface?
- Can classical geomorphological concepts such as peneplanation or retrogressive erosion be quantitatively understood? Old mountain ranges such as the Appalachian or the Urals seem to retain relief for >108 years, while subglacial fluvial valleys under Antarctica are preserved under moving ice of kilometric thickness since the Neogene. What controls the time-scale of topographic decay?[8]
- What are the erosion and transport laws governing the evolution of the Earth’s Surface?[Willenbring et al., Geology, 2013] Rivers transport sediment particles that are at the same time the tools for erosion but also the shield protecting the bedrock. How important is this double role of sediment for the evolution of landscapes?[9][10]
- How resilient is the ocean to chemical perturbations?
- What caused the huge salt deposition in the Mediterranean known as the Messinian salinity crisis? Was the Mediterranean truly desiccated? What were the effects on climate and biology, and what can we learn from extreme salt giants like this? How were the normal marine conditions reestablished?[11][12][13][14]
- There are several places where water does drain or has drained underground, but the destination is unknown. One example is “the Devil’s Kettle” in Minnesota, a pothole which swallows half of the Brule River.[15]
External links
- Open Challenges in Earth Science, from Retos Terrícolas (english).
References
- Jump up^ McKinnon, W. B. (12 April 2012). “The Strangest Terrestrial Planet”. Science 336 (6078): 162–163. doi:10.1126/science.1220825.
- Jump up^ Canup, R. M. (17 October 2012). “Forming a Moon with an Earth-like Composition via a Giant Impact”. Science 338 (6110): 1052–1055. doi:10.1126/science.1226073.
- Jump up^ George, Williams (1991). “Upper Proterozoic Tidal Rhythmites, South Australia: Sedimentary Features, Deposition, and Implications for the Earth’s Paleorotation”. Clastic Tidal Sedimentology – Memoir 16, 1991 (CSPG Special Publications): 161–177. Retrieved 3 March 2015.
- Jump up^ Wired: Was the Earth a migratory planet?
- Jump up^ Marty, B.; Zimmermann, L.; Pujol, M.; Burgess, R.; Philippot, P. (19 September 2013). “Nitrogen Isotopic Composition and Density of the Archean Atmosphere”. Science 342(6154): 101–104. doi:10.1126/science.1240971.
- Jump up^ Martin, Paula; Hunen, Jeroen van; Parman, Stephen; Davidson, Jon (1 March 2008). “Why does plate tectonics occur only on Earth?” (PDF). Physics Education 43 (2): 144–150. doi:10.1088/0031-9120/43/2/002. Retrieved 3 March 2015.
- Jump up^ Moore, William B.; Webb, A. Alexander G. (25 September 2013). “Heat-pipe Earth”. Nature 501 (7468): 501–505. doi:10.1038/nature12473. Retrieved 3 March 2015.
- Jump up^ Egholm, David L.; Knudsen, Mads F.; Sandiford, Mike (26 June 2013). “Lifespan of mountain ranges scaled by feedbacks between landsliding and erosion by rivers”. Nature498 (7455): 475–478. doi:10.1038/nature12218.
- Jump up^ Sklar, Leonard S.; Dietrich, William E. (2001). “Sediment and rock strength controls on river incision into bedrock” (PDF). Geology 29 (12): 1087. doi:10.1130/0091-7613(2001)029<1087:SARSCO>2.0.CO;2. Retrieved 3 March 2015. (effect description and tools)
- Jump up^ Cowie, Patience A.; Whittaker, Alexander C.; Attal, Mikaël; Roberts, Gerald; Tucker, Greg E.; Ganas, Athanassios (2008). “New constraints on sediment-flux–dependent river incision: Implications for extracting tectonic signals from river profiles” (PDF). Geology 36 (7): 535. doi:10.1130/G24681A.1. Retrieved 3 March 2015.(field example)
- Jump up^ Garcia-Castellanos, D.; Villaseñor, A. (14 December 2011). “Messinian salinity crisis regulated by competing tectonics and erosion at the Gibraltar arc”. Nature 480 (7377): 359–363. doi:10.1038/nature10651. PMID 22170684. Retrieved 3 March 2015. Author Publications Link
- Jump up^ Hsü, Kenneth J. (1987). The Mediterranean was a desert : a voyage of the Glomar Challenger (First Princeton paperback printing ed.). Princeton, N.J.: Princeton University Press. ISBN 978-0691024066.
- Jump up^ Clauzon, Georges; Suc, Jean-Pierre; Gautier, François; Berger, André; Loutre, Marie-France (1996). “Alternate interpretation of the Messinian salinity crisis: Controversy resolved?”. Geology 24 (4): 363. doi:10.1130/0091-7613(1996)024<0363:AIOTMS>2.3.CO;2.
- Jump up^ Krijgsman, W.; Hilgen, F. J.; Raffi, I.; Sierro, F. J.; Wilson, D. S. (12 August 1999). “Chronology, causes and progression of the Messinian salinity crisis”. Nature 400 (6745): 652–655. doi:10.1038/23231.
- Jump up^ http://www.mnn.com/earth-matters/wilderness-resources/stories/7-bizarre-places-on-earth-where-water-disappears
Unsolved Problems in Information Theory
This article lists some unsolved problems in information theory which are separated into source coding and channel coding. There are also related unsolved problems[1] in philosophy.
Channel coding
- Capacity of a network:[2] The capacity of a general wireless network is not known. There are some specific cases for which the capacity is known, such as theAWGN channel and fading channel.
- Capacity of the broadcast channel:[3][4] The capacity of the broadcast channel, or the case in which a single transmitter is sending information to many receivers is unknown in general, though it is known for several specific cases.
- Capacity of the interference channel (Two User): The capacity of the interference channel, in the case where there are two transmitter and receiver pairs that interfere among each other, is unknown in general. Capacity is known in special cases: strong interference regime, injective-deterministic. Capacity is known in approximate sense or with in a gap for: injective-semi-deterministic, additive white Gaussian noise with per block power constraint.
- Capacity of the two-way channel.[5][6] The capacity of the two-way channel (a channel in which information is sent in both directions simultaneously) is unknown.
- The capacity of Aloha:[7] The ALOHAnet used a very simple access scheme for which the capacity is still unknown, though it is known in a few special cases.
- Quantum capacity: The capacity of a quantum channel is in general not known.[8]
There are many other unsolved problems in coding theory:[9] and in other areas.[10][11]
Source coding
Distributed source coding: The best way to compress multiple correlated information sources that do not communicate with each other is not known.
References
- Jump up^ Adriaans, Pieter. “Open Problems in the Study of Information and Computation”. Retrieved 21 June 2013.
- Jump up^ Cover, Thomas. Elements of Information Theory. Wiley-Interscience. ISBN 978-0471062592.
- Jump up^ Cover, Thomas (Oct 1998). “Comments on Broadcast Channels”. IEEE Trans Inf Theory 44 (6): 2524.
- Jump up^ Sridharan, Arvind. “Broadcast Channels” (PDF). Notre Dame. Retrieved 6 July 2014.
- Jump up^ Shannon, Claude (1961). “Two-way communication channels”. Proc Fourth Berkeley sump on Mathematical Statistics and Probability 1: 611.
- Jump up^ meeuwissen, Erik (16 Aug 1998). “The Origin of Two-Way Channels”. Proc ISIT I: 185.
- Jump up^ Medard, Muriel (March 2004). “Capacity of Time-Slotted ALOHA Packetized Multiple-Access Systems Over the AWGN Channel” (PDF). EEE Transactions on Wireless COMMUNICATIONS 3 (2). Retrieved 11 July 2014.
- Jump up^ Shor, Peter (2000). “Quantum Information Theory: Results and Open Problems” (PDF). Geom. Funct. Anal.: 816–838.
- Jump up^ David Joyner; Jon-Lark Kim (2010). Selected Unsolved Problems in Coding Theory. New York: Springer.
- Jump up^ Longo, Giuseppe (1975). Information theory: new trends and open problems.
- Jump up^ Tse, David (1996). “It’s Easier to Approximate” (PDF). Information Theory Society Newsletter. Retrieved 26 June 2013.
Unsolved Problems in Linguistics
Some of the issues below are commonly recognized as unsolved problems; i.e. it is generally agreed that no solution is known. Others may be described as controversies; i.e. although there is no common agreement about the answer, there are established schools of thought that believe they have a correct answer.
Concepts
- Is there a universal definition of word?
- Is there a universal definition of sentence?
- Are there any universal grammatical categories?
- Can the elements contained in words (morphemes) and the elements contained in sentences (syntactic constituents) be shown to follow the same principles?
- How are domains for phonological processes related to syntactic structure? Do prosodic domains deviate fromsyntactic constituent structure?
- Is it possible to formally delineate languages from each other? That is to say, is it possible to use linguistic (rather than social) criteria to draw a clear boundary between two closely related languages with a dialect continuumbetween their respective standard forms (e.g. Occitan and Catalan)?
- How does grammaticalization function?
- What constitutes grammatically correct language, as viewed by native speakers of that particular language, i.e. the problem of gradient well-formedness)?
- How do creole languages emerge?
- How does lexical substitution function given the potentially limitless number of different contexts, the limits of one’s knowledge and the limits of one’s understanding and usage of language?
- How do idiolects and dialects emerge? Are there any common patterns in their development? Can they be quantitatively and qualitatively measured at all and if so, how?
Philosophy of language
- How do intension, comprehension, reference, intention and intentionality, extension, linguistic relativity, context, ambiguity, polysemy, idiolect, dialect, among other major linguistics concepts, interplay to give rise to meaningful language as spoken or written by an individual?
Languages
- Origin of language and origin of speech are major unsolved problems, despite centuries of interest in these topics.[1][2][3][4][5]
- Unclassified languages (languages whose genetic affiliation has not been established, mostly due to lack of reliable data) make up about 38 of the 6,000–7,000 languages spoken in the world.[6] An additional 45 languages are classified as language isolates, with no demonstrable relationship to other languages.[6]
- Undeciphered writing systems
- Is there an objective way to determine which are the most difficult languages?
- How accurate are linguistic typology and language classification? What are the factors that influence them?
- To what extent are conlangs usable and useful as used as natural languages by humans?
Psycholinguistics
- Language emergence:
- Language acquisition:
- Controversy: infant language acquisition / first language acquisition. How are infants able to learn language? One line of debate is between two points of view: that of psychological nativism, i.e., the language ability is somehow “hardwired” in the human brain, and that of the “tabula rasa“ or blank slate, i.e., language is acquired due to brain’s interaction with environment. Another formulation of this controversy is “nature versus nurture“.
- Is the human ability to use syntax based on innate mental structures or is syntactic speech the function of intelligence and interaction with other humans? The question is closely related to those of language emergence and acquisition.
- The language acquisition device: How localized is language in the brain? Is there a particular area in the brain responsible for the development of language abilities or is it only partially localized?
- What fundamental reasons explain why ultimate attainment in second language acquisition is typically some way short of the native speaker‘s ability, with learners varying widely in performance?
- What are the optimal ways to achieve successful second-language acquisition?
- Animals and language: How much language (e.g. syntax) can animals be taught to use? How much of animal communication can be said to have the same properties as human language (e.g. syntax)?
- What role does linguistic intuition play, how is it formed and how does it function? Is it closely linked to exposure to a unique set of different experiences and their contexts throughout one’s personal life?
Sociolinguistics
- How to deal with variation in language (including idiolects, dialects, sociolects, jargons, argots, etc.) to achieve effective and successful communication between individuals and between groups, i.e. what are the best ways to ensure efficient communication without misunderstandings: in everyday life and in educational, scientific and philosophical discussions?
- What are the best ways to quantitatively and qualitatively compare linguistic competence and linguistic performance between individuals and between groups?
- How does time (and the semantic change that it brings) and physical age influence linguistic competence?
- How are argots formed, how do they function and what are the best ways to become proficient in an argot?
- What are the relations between a standard language and its dialects?
Computational linguistics
- Is perfect computational word-sense disambiguation attainable by using software? If yes, how and why? If no, why? (This presupposes the solution to the unsolved problems in the other areas of linguistics as a basis.)
- Is accurate computational word-sense induction feasible? If yes, how and why? If not, why?
Lexicology and lexicography
- What makes a good dictionary?
- To what extent are dictionaries reliable in terms of their supposed universality when spoken language is constantly changing (semantic change, semantic extension, semantic compression, etc.)?
- What are good practices to avoid circular definitions in dictionaries? Is it possible to eliminate them at all, given the vagueness, polysemy, etc. in all languages?
- What are the best ways to ensure efficient communication without misunderstandings: in everyday life and in educational, scientific and philosophical discussions? Is total terminology standardization attainable at all? If yes, does it involve the mass use of freely available and easily accessible terminology databases?
- To what extent are termbases reliable and can their reliability be measured objectively? If yes, how and why? If no, why? What is the relationship betweentermbases and individual subjectivity and can subjectivity about word sense disambiguation be overcome at all or is it a natural result of different experiences in one’s unique personal life?
- How to successfully reduce lexicographic errors and lexicographic information costs?
Translation
- Is there an objective gauge for the quality of translation?[8]
- What are the best strategies for quality translation: fidelity or transparency, dynamic or formal equivalence, etc.?
- What are the best ways to deal with untranslatability, e.g. lexical gaps?
- How to best deal with translation loss and its accumulation, e.g. when translating from a translation (see Chinese whispers)?
- Can machine translations ever achieve the high degree of comprehensibility and quality of translations translated by a good professional human translator?
- What are the effective ways to achieve proper localization and internationalization?
References
- Jump up^ Givon, Talmy; Bertram F. Malle (2002). The Evolution of Language Out of Pre-language. John Benjamins. ISBN 1-58811-237-3.
- Jump up^ Deacon, Terrence (1997). The Symbolic Species: The Co-evolution of Language and the Brain. W.W. Norton. ISBN 0-571-17396-9.
- Jump up^ MacNeilage, Peter, 2008. The Origin of Speech. Oxford: Oxford University Press.
- Jump up^ Botha, R. and C. Knight (eds) 2009. The Cradle of Language. Oxford: Oxford University Press.
- Jump up^ Dor, D., C. Knight & J. Lewis (eds), 2014. The Social Origins of Language. Oxford: Oxford University Press.
- ^ Jump up to:a b Lewis, M. Paul, ed. (2009). Ethnologue: Languages of the World (16 ed.). Dallas: SIL International. ISBN 1-55671-216-2.
- Jump up^ “Simulated Evolution of Language: a Review of the Field”, Journal of Artificial Societies and Social Simulation vol. 5, no. 2
- Jump up^ Robert Spence, “A Functional Approach to Translation Studies. New systemic linguistic challenges in empirically informed didactics”, 2004, ISBN 3-89825-777-0, thesis. A pdf file
Unsolved Problems in Mathematics
Since the Renaissance, every century has seen the solution of more mathematical problems than the century before, and yet many mathematical problems, both major and minor, still elude solution.[1]
An unsolved problem in mathematics does not refer to the kind of problem found as an exercise in a textbook, but rather to the answer to a major question or a general method that provides a solution to an entire class of problems. Prizes are often awarded for the solution to a long-standing problem, and lists of unsolved problems receive considerable attention. This article reiterates the list of Millennium Prize Problems of unsolved problems in mathematics (includes problems ofphysics and computer science) as of August 2015, and lists further unsolved problems in algebra, additive and algebraic number theories, analysis, combinatorics,algebraic, discrete and Euclidean geometries, dynamical systems, partial differential equations, and graph, group, model, number, set and Ramsey theories, as well as miscellaneous unsolved problems. A list of problems solved since 1995 also appears, alongside some sources, general and specific, for the stated problems.
Lists of unsolved problems in mathematics
Over the course of time, several lists of unsolved mathematical problems have appeared. The following is a listing of those lists.
| List | Number of problems | Proposed by | Proposed in |
|---|---|---|---|
| Hilbert’s problems | 23 | David Hilbert | 1900 |
| Landau’s problems | 4 | Edmund Landau | 1912 |
| Taniyama’s problems[2] | 36 | Yutaka Taniyama | 1955 |
| Thurston’s 24 questions[3][4] | 24 | William Thurston | 1982 |
| Smale’s problems | 18 | Stephen Smale | 1998 |
| Millennium Prize problems | 7 | Clay Mathematics Institute | 2000 |
| Unsolved Problems in Mathematics for the 21st Century[5] | 22 | Jair Minoro Abe, Shotaro Tanaka | 2001 |
| DARPA’s math challenges[6][7] | 23 | DARPA | 2007 |
Millennium Prize Problems
Of the original seven Millennium Prize Problems set by the Clay Mathematics Institute, six have yet to be solved, as of 2016:[8]
- P versus NP
- Hodge conjecture
- Riemann hypothesis
- Yang–Mills existence and mass gap
- Navier–Stokes existence and smoothness
- Birch and Swinnerton-Dyer conjecture
The seventh problem, the Poincaré conjecture, has been solved.[9] The smooth four-dimensional Poincaré conjecture—that is, whether a four-dimensional topological sphere can have two or more inequivalent smooth structures—is still unsolved.[10]
Unsolved problems
Additive number theory
- Beal’s conjecture
- Fermat–Catalan conjecture
- Goldbach’s conjecture
- The values of g(k) and G(k) in Waring’s problem
- Collatz conjecture (3n + 1 conjecture)
- Lander, Parkin, and Selfridge conjecture
- Diophantine quintuples
- Gilbreath’s conjecture
- Erdős conjecture on arithmetic progressions
- Erdős–Turán conjecture on additive bases
- Pollock octahedral numbers conjecture
- Skolem problem
- Determine growth rate of rk(N) (see Szemerédi’s theorem)
- Minimum overlap problem
Algebra
- Homological conjectures in commutative algebra
- Hilbert’s sixteenth problem
- Hilbert’s fifteenth problem
- Hadamard conjecture
- Jacobson’s conjecture
- Existence of perfect cuboids and associated Cuboid conjectures
- Zauner’s conjecture: existence of SIC-POVMs in all dimensions
- Wild Problem: Classification of pairs of n×n matrices under simultaneous conjugation and problems containing it such as a lot of classification problems
- Köthe conjecture
- Birch–Tate conjecture
- Serre’s conjecture II
- Bombieri–Lang conjecture
- Farrell–Jones conjecture
- Bost conjecture
- Uniformity conjecture
- Kaplansky’s conjecture
- Kummer–Vandiver conjecture
- Serre’s multiplicity conjectures
- Pierce–Birkhoff conjecture
- Eilenberg–Ganea conjecture
- Green’s conjecture
- Grothendieck–Katz p-curvature conjecture
- Sendov’s conjecture
Algebraic geometry
- André–Oort conjecture
- Bass conjecture
- Deligne conjecture
- Fröberg conjecture
- Fujita conjecture
- Hartshorne conjectures
- Manin conjecture
- Nakai conjecture
- Resolution of singularities in characteristic p
- Standard conjectures on algebraic cycles
- Section conjecture
- Tate conjecture
- Virasoro conjecture
- Whitehead conjecture
- Zariski multiplicity conjecture
Algebraic number theory
- Are there infinitely many real quadratic number fields with unique factorization (Class number problem)?
- Characterize all algebraic number fields that have some power basis.
- Stark conjectures (including Brumer–Stark conjecture)
Analysis
- The Jacobian conjecture
- Schanuel’s conjecture and four exponentials conjecture
- Lehmer’s conjecture
- Pompeiu problem
- Are
 (the Euler–Mascheroni constant), π + e, π − e, πe, π/e, πe, π√2, ππ, eπ2, ln π, 2e, ee, Catalan’s constant or Khinchin’s constant rational, algebraic irrational, or transcendental? What is the irrationality measure of each of these numbers?[11][12][13]
(the Euler–Mascheroni constant), π + e, π − e, πe, π/e, πe, π√2, ππ, eπ2, ln π, 2e, ee, Catalan’s constant or Khinchin’s constant rational, algebraic irrational, or transcendental? What is the irrationality measure of each of these numbers?[11][12][13] - Khabibullin’s conjecture on integral inequalities
- Hilbert’s thirteenth problem
- Vitushkin’s conjecture
Combinatorics
- Number of magic squares (sequence A006052 in OEIS)
- Number of magic tori (sequence A270876 in OEIS)
- Finding a formula for the probability that two elements chosen at random generate the symmetric group

- Frankl’s union-closed sets conjecture: for any family of sets closed under sums there exists an element (of the underlying space) belonging to half or more of the sets
- The lonely runner conjecture: if
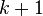 runners with pairwise distinct speeds run round a track of unit length, will every runner be “lonely” (that is, be at least a distance
runners with pairwise distinct speeds run round a track of unit length, will every runner be “lonely” (that is, be at least a distance  from each other runner) at some time?
from each other runner) at some time? - Singmaster’s conjecture: is there a finite upper bound on the multiplicities of the entries greater than 1 in Pascal’s triangle?
- The 1/3–2/3 conjecture: does every finite partially ordered set that is not totally ordered contain two elements x and y such that the probability that x appears before y in a random linear extension is between 1/3 and 2/3?
- unicity conjecture for Markov numbers
- balance puzzle [14]
Discrete geometry
- Solving the happy ending problem for arbitrary

- Finding matching upper and lower bounds for k-sets and halving lines
- The Hadwiger conjecture on covering n-dimensional convex bodies with at most 2n smaller copies
- The Kobon triangle problem on triangles in line arrangements
- The McMullen problem on projectively transforming sets of points into convex position
- Ulam’s packing conjecture about the identity of the worst-packing convex solid
- Filling area conjecture
- Hopf conjecture
- Kakeya conjecture
Euclidean geometry
- The einstein problem – does there exist a two-dimensional shape that forms the prototile for an aperiodic tiling, but not for any periodic tiling?[15]
- Inscribed square problem – does every Jordan curve have an inscribed square?[16]
- Moser’s worm problem – what is the smallest area of a shape that can cover every unit-length curve in the plane?[17]
- The moving sofa problem – what is the largest area of a shape that can be maneuvered through a unit-width L-shaped corridor?[18]
- Shephard’s problem (a.k.a. Dürer’s conjecture) – does every convex polyhedron have a net?[19]
- The Thomson problem – what is the minimum energy configuration of N particles bound to the surface of a unit sphere that repel each other with a 1/r potential (or any potential in general)?
- Pentagonal tiling – 15 types of convex pentagons are known to monohedrally tile the plane, and it is not known whether this list is complete.[20]
- Falconer’s conjecture
- g-conjecture
- Circle packing in an equilateral triangle
- Circle packing in an isosceles right triangle
Dynamical systems
- Furstenberg conjecture – Is every invariant and ergodic measure for the
 action on the circle either Lebesgue or atomic?
action on the circle either Lebesgue or atomic? - Margulis conjecture — Measure classification for diagonalizable actions in higher-rank groups
- MLC conjecture – Is the Mandelbrot set locally connected ?
- Weinstein conjecture – Does a regular compact contact type level set of a Hamiltonian on a symplectic manifold carry at least one periodic orbit of the Hamiltonian flow?
- Is every reversible cellular automaton in three or more dimensions locally reversible?[21]
Graph theory
- Barnette’s conjecture that every cubic bipartite three-connected planar graph has a Hamiltonian cycle
- The Erdős–Gyárfás conjecture on cycles with power-of-two lengths in cubic graphs
- The Erdős–Hajnal conjecture on finding large homogeneous sets in graphs with a forbidden induced subgraph
- The Hadwiger conjecture relating coloring to clique minors
- The Erdős–Faber–Lovász conjecture on coloring unions of cliques
- Harborth’s conjecture that every planar graph can be drawn with integer edge lengths
- The total coloring conjecture
- Hadwiger conjecture (graph theory)
- The list coloring conjecture
- The Ringel–Kotzig conjecture on graceful labeling of trees
- How many unit distances can be determined by a set of n points? (see Counting unit distances)
- The Hadwiger–Nelson problem on the chromatic number of unit distance graphs
- Lovász conjecture
- Deriving a closed-form expression for the percolation threshold values, especially
 (square site)
(square site) - Tutte’s conjectures that every bridgeless graph has a nowhere-zero 5-flow and every bridgeless graph without the Petersen graph as a minor has a nowhere-zero 4-flow
- Petersen coloring conjecture
- The reconstruction conjecture and new digraph reconstruction conjecture concerning whether or not a graph is recognizable by the vertex deleted subgraphs.
- The cycle double cover conjecture that every bridgeless graph has a family of cycles that includes each edge twice.
- Does a Moore graph with girth 5 and degree 57 exist?
- Conway’s thrackle conjecture
- Negami’s conjecture on the characterization of graphs with planar covers
- The Blankenship–Oporowski conjecture on the book thickness of subdivisions
- Hedetniemi’s conjecture
- Vizing’s conjecture
Group theory
- Is every finitely presented periodic group finite?
- The inverse Galois problem: is every finite group the Galois group of a Galois extension of the rationals?
- For which positive integers m, n is the free Burnside group B(m,n) finite? In particular, is B(2, 5) finite?
- Is every group surjunctive?
- Andrews–Curtis conjecture
- Herzog–Schönheim conjecture
- Does generalized moonshine exist?
Model theory
- Vaught’s conjecture
- The Cherlin–Zilber conjecture: A simple group whose first-order theory is stable in
 is a simple algebraic group over an algebraically closed field.
is a simple algebraic group over an algebraically closed field. - The Main Gap conjecture, e.g. for uncountable first order theories, for AECs, and for
 -saturated models of a countable theory.[22]
-saturated models of a countable theory.[22] - Determine the structure of Keisler’s order[23][24]
- The stable field conjecture: every infinite field with a stable first-order theory is separably closed.
- Is the theory of the field of Laurent series over
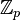 decidable? of the field of polynomials over
decidable? of the field of polynomials over  ?
? - (BMTO) Is the Borel monadic theory of the real order decidable? (MTWO) Is the monadic theory of well-ordering consistently decidable?[25]
- The Stable Forking Conjecture for simple theories[26]
- For which number fields does Hilbert’s tenth problem hold?
- Assume K is the class of models of a countable first order theory omitting countably many types. If K has a model of cardinality
 does it have a model of cardinality continuum?[27]
does it have a model of cardinality continuum?[27] - Shelah’s eventual Categority conjecture: For every cardinal \lambda there exists a cardinal \mu(\lambda) such that If an AEC K with LS(K)<= \lambda is categorical in a cardinal above \mu(\lambda) then it is categorical in all cardinals above \mu(\lambda).[22][28]
- Shelah’s categoricity conjecture for L_{\omega_1,\omega}: If a sentence is categorical above the Hanf number then it is categorical in all cardinals above the Hanf number.[22]
- Is there a logic L which satisfies both the Beth property and Δ-interpolation, is compact but does not satisfy the interpolation property?[29]
- If the class of atomic models of a complete first order theory is categorical in the
 , is it categorical in every cardinal?[30][31]
, is it categorical in every cardinal?[30][31] - Is every infinite, minimal field of characteristic zero algebraically closed? (minimal = no proper elementary substructure)
- Kueker’s conjecture[32]
- Does there exist an o-minimal first order theory with a trans-exponential (rapid growth) function?
- Lachlan’s decision problem
- Does a finitely presented homogeneous structure for a finite relational language have finitely many reducts?
- Do the Henson graphs have the finite model property? (e.g. triangle-free graphs)
- The universality problem for C-free graphs: For which finite sets C of graphs does the class of C-free countable graphs have a universal member under strong embeddings?[33]
- The universality spectrum problem: Is there a first-order theory whose universality spectrum is minimum?[34]
Number theory (general)
- Grand Riemann hypothesis
- n conjecture
- abc conjecture (Proof claimed in 2012, currently under review.)
- Hilbert’s ninth problem
- Hilbert’s eleventh problem
- Hilbert’s twelfth problem
- Carmichael’s totient function conjecture
- Erdős–Straus conjecture
- Pillai’s conjecture
- Hall’s conjecture
- Lindelöf hypothesis
- Montgomery’s pair correlation conjecture
- Hilbert–Pólya conjecture
- Grimm’s conjecture
- Leopoldt’s conjecture
- Do any odd perfect numbers exist?
- Are there infinitely many perfect numbers?
- Do quasiperfect numbers exist?
- Do any odd weird numbers exist?
- Do any Lychrel numbers exist?
- Is 10 a solitary number?
- Catalan–Dickson conjecture on aliquot sequences
- Do any Taxicab(5, 2, n) exist for n>1?
- Brocard’s problem: existence of integers, (n,m), such that n!+1 = m2 other than n=4, 5, 7
- Beilinson conjecture
- Littlewood conjecture
- Szpiro’s conjecture
- Vojta’s conjecture
- Goormaghtigh conjecture
- Congruent number problem (a corollary to Birch and Swinnerton-Dyer conjecture, per Tunnell’s theorem)
- Lehmer’s totient problem: if φ(n) divides n − 1, must n be prime?
- Are there infinitely many amicable numbers?
- Are there any pairs of amicable numbers which have opposite parity?
- Are there any pairs of relatively prime amicable numbers?
- Are there infinitely many betrothed numbers?
- Are there any pairs of betrothed numbers which have same parity?
- The Gauss circle problem – how far can the number of integer points in a circle centered at the origin be from the area of the circle?
- Is π a normal number (its digits are “random”)?[35]
- Casas-Alvero conjecture
- Sato–Tate conjecture
- Find value of De Bruijn–Newman constant
Number theory (prime numbers)
- Catalan’s Mersenne conjecture
- Agoh–Giuga conjecture
- The Gaussian moat problem: is it possible to find an infinite sequence of distinct Gaussian prime numbers such that the difference between consecutive numbers in the sequence is bounded?
- New Mersenne conjecture
- Erdős–Mollin–Walsh conjecture
- Are there infinitely many prime quadruplets?
- Are there infinitely many cousin primes?
- Are there infinitely many sexy primes?
- Are there infinitely many Mersenne primes (Lenstra–Pomerance–Wagstaff conjecture); equivalently, infinitely many even perfect numbers?
- Are there infinitely many Wagstaff primes?
- Are there infinitely many Sophie Germain primes?
- Are there infinitely many Pierpont primes?
- Are there infinitely many regular primes, and if so is their relative density
 ?
? - Are there infinitely many repunit primes to every base except perfect power and numbers of the form -4k4?
- Are there infinitely many Cullen primes?
- Are there infinitely many Woodall primes?
- Are there infinitely many palindromic primes to every base?
- Are there infinitely many Fibonacci primes?
- Are there infinitely many Lucas primes?
- Are there infinitely many Pell primes?
- Are there infinitely many Newman–Shanks–Williams primes?
- Are all Mersenne numbers of prime index square-free?
- Are there infinitely many Wieferich primes?
- Are there any Wieferich primes in base 47?
- Are there any composite c satisfying 2c – 1 ≡ 1 (mod c2)?
- For any given integer a > 0, are there infinitely many primes p such that ap – 1 ≡ 1 (mod p2)?[36]
- Can a prime p satisfy 2p − 1 ≡ 1 (mod p2) and 3p − 1 ≡ 1 (mod p2) simultaneously?[37]
- Are there infinitely many Wilson primes?
- Are there infinitely many Wolstenholme primes?
- Are there any Wall–Sun–Sun primes?
- Is every Fermat number 22n + 1 composite for
 ?
? - Are all Fermat numbers square-free?
- For any given integer a which is not a square and does not equal to -1, are there infinitely many primes with a as a primitive root?
- Artin’s conjecture on primitive roots
- Is 78,557 the lowest Sierpiński number (so-called Selfridge’s conjecture)?
- Is 509,203 the lowest Riesel number?
- Fortune’s conjecture (that no Fortunate number is composite)
- Landau’s problems
- Does every prime number appear in the Euclid–Mullin sequence?
- Does the converse of Wolstenholme’s theorem hold for all natural numbers?
- Elliott–Halberstam conjecture
- Problems associated to Linnik’s theorem
Partial differential equations
- Regularity of solutions of Vlasov–Maxwell equations
- Regularity of solutions of Euler equations
Ramsey theory
- The values of the Ramsey numbers, particularly

- The values of the Van der Waerden numbers
- Erdős–Burr conjecture
Set theory
- The problem of finding the ultimate core model, one that contains all large cardinals.
- If ℵω is a strong limit cardinal, then 2ℵω < ℵω1 (see Singular cardinals hypothesis). The best bound, ℵω4, was obtained by Shelah using his pcf theory.
- Woodin’s Ω-hypothesis.
- Does the consistency of the existence of a strongly compact cardinal imply the consistent existence of a supercompact cardinal?
- (Woodin) Does the Generalized Continuum Hypothesis below a strongly compact cardinal imply the Generalized Continuum Hypothesis everywhere?
- Does there exist a Jónsson algebra on ℵω?
- Without assuming the axiom of choice, can a nontrivial elementary embedding V→V exist?
- Does the Generalized Continuum Hypothesis entail
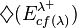 for every singular cardinal
for every singular cardinal  ?
? - Does the Generalized Continuum Hypothesis imply the existence of an ℵ2-Suslin tree?
Other
- Problems in loop theory and quasigroup theory
- Problems in Latin squares
- List of unsolved problems in statistics
- List of unsolved problems in computer science
- Invariant subspace problem
- Kaplansky’s conjectures on groups rings
- Painlevé conjecture
- Dixmier conjecture
- Baum–Connes conjecture
- Novikov conjecture
- Prove Turing completeness for all unique elementary cellular automaton
- Generalized star height problem
- Assorted sphere packing problems, e.g. the densest irregular hypersphere packings
- Closed curve problem: Find (explicit) necessary and sufficient conditions that determine when, given two periodic functions with the same period, the integral curve is closed.[38]
- Keating–Snaith conjecture
- Kung-Traub conjecture
- Atiyah conjecture on configurations
- Toeplitz’ conjecture (open since 1911)
- Carathéodory conjecture
- Church–Turing thesis
- Weight-monodromy conjecture
- Berry–Tabor conjecture
- Birkhoff conjecture
- Guralnick–Thompson conjecture
- Hilbert–Smith conjecture
- MNOP conjecture
- Mazur’s conjectures
- Rendezvous problem
- Scholz conjecture
- Nirenberg–Treves conjecture
- Quantum unique ergodicity conjecture
- Density hypothesis
- Zhou conjecture
- Borel conjecture
Problems solved since 1995
- Boolean Pythagorean triples problem (Marijn Heule, Oliver Kullmann, Victor Marek, 2016)[39]
- Main conjecture in Vinogradov’s mean-value theorem (Jean Bourgain, Ciprian Demeter, Larry Guth, 2015)[40]
- Erdős discrepancy problem (Terence Tao, 2015)[41]
- Umbral moonshine conjecture (John F. R. Duncan, Michael J. Griffin, Ken Ono, 2015)[42]
- Anderson conjecture (Cheeger, Naber, 2014)[43]
- Goldbach’s weak conjecture (Harald Helfgott, 2013)[44][45][46]
- Kadison–Singer problem (Adam Marcus, Daniel Spielman and Nikhil Srivastava, 2013)[47][48] (and the Feichtinger’s conjecture, Anderson’s paving conjectures, Weaver’s discrepancy theoretic
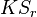 and
and  conjectures, Bourgain-Tzafriri conjecture and
conjectures, Bourgain-Tzafriri conjecture and  -conjecture)
-conjecture) - Virtual Haken conjecture (Agol, Groves, Manning, 2012)[49] (and by work of Wise also virtually fibered conjecture)
- Hsiang–Lawson’s conjecture (Brendle, 2012)[50]
- Willmore conjecture (Fernando Codá Marques and André Neves, 2012)[51]
- Ehrenpreis conjecture (Kahn, Markovic, 2011)[52]
- Hanna Neumann conjecture (Mineyev, 2011)[53]
- Bloch–Kato conjecture (Voevodsky, 2011)[54] (and Quillen–Lichtenbaum conjecture and by work of Geisser and Levine (2001) also Beilinson–Lichtenbaum conjecture[55][56][57])
- Erdős distinct distances problem (Larry Guth, Netz Hawk Katz, 2011)[58]
- Density theorem (Namazi, Souto, 2010)[59]
- Hirsch conjecture (Francisco Santos Leal, 2010)[60][61]
- Sidon set problem (J. Cilleruelo, I. Ruzsa and C. Vinuesa, 2010)[62]
- Atiyah conjecture (Austin, 2009)[63]
- Kauffman–Harary conjecture (Matmann, Solis, 2009)[64]
- Surface subgroup conjecture (Kahn, Markovic, 2009)[65]
- Scheinerman’s conjecture (Jeremie Chalopin and Daniel Gonçalves, 2009)[66]
- Geometrization conjecture (proof was completed by Morgan and Tian in 2008[67] and it is based mostly on work of Grigori Perelman, 2002)[68]
- Serre’s modularity conjecture (Chandrashekhar Khare and Jean-Pierre Wintenberger, 2008)[69][70][71]
- Heterogeneous tiling conjecture (squaring the plane) (Frederick V. Henle and James M. Henle, 2008)[72]
- Erdős–Menger conjecture (Aharoni, Berger 2007)[73]
- Road coloring conjecture (Avraham Trahtman, 2007)[74]
- The angel problem (Various independent proofs, 2006)[75][76][77][78]
- Lax conjecture (Lewis, Parrilo, Ramana, 2005)[79]
- The Langlands–Shelstad fundamental lemma (Ngô Bảo Châu and Gérard Laumon, 2004)[80]
- Tameness conjecture and Ahlfors measure conjecture (Ian Agol, 2004)[81]
- Robertson–Seymour theorem (Robertson, Seymour, 2004)[82]
- Stanley–Wilf conjecture (Gábor Tardos and Adam Marcus, 2004)[83] (and also Alon–Friedgut conjecture)
- Green–Tao theorem (Ben J. Green and Terence Tao, 2004)[84]
- Ending lamination theorem (Jeffrey F. Brock, Richard D. Canary, Yair N. Minsky, 2004)[85]
- Cameron–Erdős conjecture (Ben J. Green, 2003, Alexander Sapozhenko, 2003)[86][87]
- Milnor conjecture (Vladimir Voevodsky, 2003)[88]
- Kemnitz’s conjecture (Reiher, 2003, di Fiore, 2003)[89]
- Nagata’s conjecture (Shestakov, Umirbaev, 2003)[90]
- Kirillov’s conjecture (Baruch, 2003)[91]
- Poincaré conjecture (Grigori Perelman, 2002)[68]
- Strong perfect graph conjecture (Maria Chudnovsky, Neil Robertson, Paul Seymour and Robin Thomas, 2002)[92]
- Kouchnirenko’s conjecture (Haas, 2002)[93]
- Vaught conjecture (Knight, 2002)[94]
- Double bubble conjecture (Hutchings, Morgan, Ritoré, Ros, 2002)[95]
- Catalan’s conjecture (Preda Mihăilescu, 2002)[96]
- n! conjecture (Haiman, 2001)[97] (and also Macdonald positivity conjecture)
- Kato’s conjecture (Auscher, Hofmann, Lacey, McIntosh and Tchamitchian, 2001)[98]
- Deligne’s conjecture on 1-motives (Luca Barbieri-Viale, Andreas Rosenschon, Morihiko Saito, 2001)[99]
- Modularity theorem (Breuil, Conrad, Diamond and Taylor, 2001)[100]
- Erdős–Stewart conjecture (Florian Luca, 2001)[101]
- Berry–Robbins problem (Atiyah, 2000)[102]
- Erdős–Graham problem (Croot, 2000)[103]
- Honeycomb conjecture (Thomas Hales, 1999)[104]
- Gradient conjecture (Krzysztof Kurdyka, Tadeusz Mostowski, Adam Parusinski, 1999)[105]
- Bogomolov conjecture (Emmanuel Ullmo, 1998, Shou-Wu Zhang, 1998)[106][107]
- Lafforgue’s theorem (Laurent Lafforgue, 1998)[108]
- Kepler conjecture (Ferguson, Hales, 1998)[109]
- Dodecahedral conjecture (Hales, McLaughlin, 1998)[110]
- Ganea conjecture (Iwase, 1997)[111]
- Torsion conjecture (Merel, 1996)[112]
- Harary’s conjecture (Chen, 1996)[113]
- Fermat’s Last Theorem (Andrew Wiles and Richard Taylor, 1995)[114][115]
References
- Jump up^ Eves, An Introduction to the History of Mathematics 6th Edition, Thomson, 1990,ISBN 978-0-03-029558-4.
- Jump up^ Shimura, G. (1989). “Yutaka Taniyama and his time”. Bulletin of the London Mathematical Society 21 (2): 186–196. doi:10.1112/blms/21.2.186.
- Jump up^ http://www.uni-regensburg.de/Fakultaeten/nat_Fak_I/friedl/papers/dmv_091514.pdf
- Jump up^ THREE DIMENSIONAL MANIFOLDS, KLEINIAN GROUPS AND HYPERBOLIC GEOMETRY
- Jump up^ Abe, Jair Minoro; Tanaka, Shotaro (2001). Unsolved Problems in Mathematics for the 21st Century. IOS Press. ISBN 9051994907.
- Jump up^ “DARPA invests in math”. CNN. 2008-10-14. Archived from the original on 2009-03-04. Retrieved 2013-01-14.
- Jump up^ “Broad Agency Announcement (BAA 07-68) for Defense Sciences Office (DSO)”. DARPA. 2007-09-10. Archived from the original on 2012-10-01. Retrieved 2013-06-25.
- Jump up^ “Millennium Problems”.
- Jump up^ “Poincaré Conjecture”. Clay Mathematics Institute. Archived from the originalon 2013-12-15.
- Jump up^ “Smooth 4-dimensional Poincare conjecture”.
- Jump up^ For background on the numbers that are the focus of this problem, see articles by Eric W. Weisstein, on pi ([1]), e ([2]), Khinchin’s Constant ([3]), irrational numbers ([4]), transcendental numbers ([5]), and irrationality measures ([6]) at Wolfram MathWorld, all articles accessed 15 December 2014.
- Jump up^ Michel Waldschmidt, 2008, “An introduction to irrationality and transcendence methods,” at The University of Arizona The Southwest Center for Arithmetic Geometry 2008 Arizona Winter School, March 15–19, 2008 (Special Functions and Transcendence), see [7], accessed 15 December 2014.
- Jump up^ John Albert, posting date unknown, “Some unsolved problems in number theory” [from Victor Klee & Stan Wagon, “Old and New Unsolved Problems in Plane Geometry and Number Theory”], in University of Oklahoma Math 4513 course materials, see [8], accessed 15 December 2014.
- Jump up^ Solution to the Counterfeit Coin Problem and its Generalization
- Jump up^ Socolar, Joshua E. S.; Taylor, Joan M. (2012), “Forcing nonperiodicity with a single tile”, The Mathematical Intelligencer 34 (1): 18–28, arXiv:1009.1419,doi:10.1007/s00283-011-9255-y, MR 2902144
- Jump up^ Matschke, Benjamin (2014), “A survey on the square peg problem”, Notices of the American Mathematical Society 61 (4): 346–253, doi:10.1090/noti1100
- Jump up^ Norwood, Rick; Poole, George; Laidacker, Michael (1992), “The worm problem of Leo Moser”, Discrete and Computational Geometry 7 (2): 153–162,doi:10.1007/BF02187832, MR 1139077
- Jump up^ Wagner, Neal R. (1976), “The Sofa Problem” (PDF), The American Mathematical Monthly 83 (3): 188–189, doi:10.2307/2977022,JSTOR 2977022
- Jump up^ Demaine, Erik D.; O’Rourke, Joseph (2007), “Chapter 22. Edge Unfolding of Polyhedra”, Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Cambridge University Press, pp. 306–338
- Jump up^ Bellos, Alex (11 August 2015), “Attack on the pentagon results in discovery of new mathematical tile”, The Guardian
- Jump up^ Kari, Jarkko (2009), “Structure of reversible cellular automata”, Unconventional Computation: 8th International Conference, UC 2009, Ponta Delgada, Portugal, September 7ÔÇô11, 2009, Proceedings, Lecture Notes in Computer Science 5715, Springer, p. 6, doi:10.1007/978-3-642-03745-0_5
- ^ Jump up to:a b c Shelah S, Classification Theory, North-Holland, 1990
- Jump up^ Keisler, HJ, “Ultraproducts which are not saturated.” J. Symb Logic 32 (1967) 23—46.
- Jump up^ Malliaris M, Shelah S, “A dividing line in simple unstable theories.”http://arxiv.org/abs/1208.2140
- Jump up^ Gurevich, Yuri, “Monadic Second-Order Theories,” in J. Barwise, S. Feferman, eds., Model-Theoretic Logics (New York: Springer-Verlag, 1985), 479–506.
- Jump up^ Peretz, Assaf, “Geometry of forking in simple theories.” J. Symbolic Logic Volume 71, Issue 1 (2006), 347–359.
- Jump up^ Shelah, Saharon (1999). “Borel sets with large squares”. Fundamenta Mathematicae 159 (1): 1–50. arXiv:math/9802134.
- Jump up^ Shelah, Saharon (2009). Classification theory for abstract elementary classes. College Publications. ISBN 978-1-904987-71-0.
- Jump up^ Makowsky J, “Compactness, embeddings and definability,” in Model-Theoretic Logics, eds Barwise and Feferman, Springer 1985 pps. 645–715.
- Jump up^ Baldwin, John T. (July 24, 2009). Categoricity (PDF). American Mathematical Society. ISBN 978-0821848937. Retrieved February 20, 2014.
- Jump up^ Shelah, Saharon. “Introduction to classification theory for abstract elementary classes”.
- Jump up^ Hrushovski, Ehud, “Kueker’s conjecture for stable theories.” Journal of Symbolic Logic Vol. 54, No. 1 (Mar., 1989), pp. 207–220.
- Jump up^ Cherlin, G.; Shelah, S. (May 2007). “Universal graphs with a forbidden subtree”.Journal of Combinatorial Theory, Series B 97 (3): 293–333. arXiv:math/0512218.doi:10.1016/j.jctb.2006.05.008.
- Jump up^ Džamonja, Mirna, “Club guessing and the universal models.” On PCF, ed. M. Foreman, (Banff, Alberta, 2004).
- Jump up^ “Are the Digits of Pi Random? Berkeley Lab Researcher May Hold Key”.
- Jump up^ Ribenboim, P. (2006). Die Welt der Primzahlen (in German) (2nd ed.). Springer. pp. 242–243. doi:10.1007/978-3-642-18079-8. ISBN 978-3-642-18078-1.
- Jump up^ Dobson, J. B. (June 2012) [2011], On Lerch’s formula for the Fermat quotient, p. 15, arXiv:1103.3907
- Jump up^ Barros, Manuel (1997), “General Helices and a Theorem of Lancret”, American Mathematical Society 125: 1503–1509, JSTOR 2162098
- Jump up^ http://arxiv.org/pdf/1605.00723v1.pdf
- Jump up^ Bourgain, Jean; Ciprian, Demeter; Larry, Guth (2015). “Proof of the main conjecture in Vinogradov’s Mean Value Theorem for degrees higher than three”.Annals of Mathematics.
- Jump up^ http://arxiv.org/pdf/1509.05363v5.pdf
- Jump up^ Proof of the umbral moonshine conjecture – Springer
- Jump up^ http://arxiv.org/pdf/1406.6534v10.pdf
- Jump up^ Helfgott, Harald A. (2013). “Major arcs for Goldbach’s theorem”.arXiv:1305.2897 [math.NT].
- Jump up^ Helfgott, Harald A. (2012). “Minor arcs for Goldbach’s problem”.arXiv:1205.5252 [math.NT].
- Jump up^ Helfgott, Harald A. (2013). “The ternary Goldbach conjecture is true”.arXiv:1312.7748 [math.NT].
- Jump up^ Casazza, Peter G.; Fickus, Matthew; Tremain, Janet C.; Weber, Eric (2006). Han, Deguang; Jorgensen, Palle E. T.; Larson, David Royal, eds. “The Kadison-Singer problem in mathematics and engineering: A detailed account”.Contemporary Mathematics. Large Deviations for Additive Functionals of Markov Chains: The 25th Great Plains Operator Theory Symposium, June 7–12, 2005, University of Central Florida, Florida (American Mathematical Society.) 414: 299–355. doi:10.1090/conm/414/07820. ISBN 978-0-8218-3923-2. Retrieved 24 April2015.
- Jump up^ Mackenzie, Dana. “Kadison–Singer Problem Solved” (PDF). SIAM News(January/February 2014) (Society for Industrial and Applied Mathematics). Retrieved 24 April 2015.
- Jump up^ http://arxiv.org/pdf/1204.2810v1.pdf
- Jump up^ http://www.math.jhu.edu/~js/Math646/brendle.lawson.pdf
- Jump up^ Marques, Fernando C.; Neves, André (2013). “Min-max theory and the Willmore conjecture”. Annals of Mathematics. arXiv:1202.6036.doi:10.4007/annals.2014.179.2.6.
- Jump up^ http://arxiv.org/pdf/1101.1330v4.pdf
- Jump up^ http://www.math.uiuc.edu/~mineyev/math/art/submult-shnc.pdf
- Jump up^ http://annals.math.princeton.edu/wp-content/uploads/annals-v174-n1-p11-p.pdf
- Jump up^ https://www.uni-due.de/~bm0032/publ/BlochKato.pdf
- Jump up^ page 359
- Jump up^ “motivic cohomology – Milnor-Bloch-Kato conjecture implies the Beilinson-Lichtenbaum conjecture – MathOverflow”.
- Jump up^ http://arxiv.org/pdf/1011.4105v3.pdf
- Jump up^ https://www.researchgate.net/profile/Juan_Souto3/publication/228365532_Non-realizability_and_ending_laminations_Proof_of_the_Density_Conjecture/links/541d85a10cf2218008d1d2e5.pdf
- Jump up^ Santos, Franciscos (2012). “A counterexample to the Hirsch conjecture”. Annals of Mathematics (Princeton University and Institute for Advanced Study) 176 (1): 383–412. doi:10.4007/annals.2012.176.1.7.
- Jump up^ Ziegler, Günter M. (2012). “Who solved the Hirsch conjecture?”. Documenta Mathematica. Extra Volume “Optimization Stories”: 75–85.
- Jump up^ “Generalized Sidon sets”.
- Jump up^ http://arxiv.org/pdf/0909.2360v3.pdf
- Jump up^ http://arxiv.org/pdf/0906.1612v2.pdf
- Jump up^ http://arxiv.org/pdf/0910.5501v5.pdf
- Jump up^ http://www.csie.ntu.edu.tw/~hil/bib/ChalopinG09.pdf
- Jump up^ http://arxiv.org/pdf/0809.4040.pdf
- ^ Jump up to:a b “Prize for Resolution of the Poincaré Conjecture Awarded to Dr. Grigoriy Perelman” (PDF) (Press release). Clay Mathematics Institute. March 18, 2010. Retrieved November 13, 2015.
The Clay Mathematics Institute hereby awards the Millennium Prize for resolution of the Poincaré conjecture to Grigoriy Perelman.
- Jump up^ Khare, Chandrashekhar; Wintenberger, Jean-Pierre (2009), “Serre’s modularity conjecture (I)”, Inventiones Mathematicae 178 (3): 485–504, doi:10.1007/s00222-009-0205-7
- Jump up^ Khare, Chandrashekhar; Wintenberger, Jean-Pierre (2009), “Serre’s modularity conjecture (II)”, Inventiones Mathematicae 178 (3): 505–586, doi:10.1007/s00222-009-0206-6
- Jump up^ “2011 Cole Prize in Number Theory” (PDF). Notices of the AMS (Providence, Rhode Island, United States: American Mathematical Society) 58 (4): 610–611.ISSN 1088-9477. OCLC 34550461.
- Jump up^ http://www.ww.amc12.org/sites/default/files/pdf/pubs/SquaringThePlane.pdf
- Jump up^ http://arxiv.org/pdf/math/0509397.pdf
- Jump up^ Seigel-Itzkovich, Judy (2008-02-08). “Russian immigrant solves math puzzle”. The Jerusalem Post. Retrieved 2015-11-12.
- Jump up^ http://homepages.warwick.ac.uk/~masgak/papers/bhb-angel.pdf
- Jump up^ http://home.broadpark.no/~oddvark/angel/Angel.pdf
- Jump up^ http://homepages.warwick.ac.uk/~masibe/angel-mathe.pdf
- Jump up^ http://www.cs.bu.edu/~gacs/papers/angel.pdf
- Jump up^ http://www.ams.org/journals/proc/2005-133-09/S0002-9939-05-07752-X/S0002-9939-05-07752-X.pdf
- Jump up^ “Fields Medal – Ngô Bảo Châu”. International Congress of Mathematicians 2010. ICM. 19 August 2010. Retrieved 2015-11-12.
Ngô Bảo Châu is being awarded the 2010 Fields Medal for his proof of the Fundamental Lemma in the theory of automorphic forms through the introduction of new algebro-geometric methods.
- Jump up^ http://arxiv.org/pdf/math/0405568v1.pdf
- Jump up^ “Graph Theory”.
- Jump up^ Chung, Fan; Greene, Curtis; Hutchinson, Joan (April 2015). “Herbert S. Wilf (1931–2012)” (PDF). Notices of the AMS (Providence, Rhode Island, United States: American Mathematical Society) 62 (4): 358. ISSN 1088-9477.OCLC 34550461.
The conjecture was finally given an exceptionally elegant proof by A. Marcus and G. Tardos in 2004.
- Jump up^ “Bombieri and Tao Receive King Faisal Prize” (PDF). Notices of the AMS(Providence, Rhode Island, United States: American Mathematical Society) 57 (5): 642–643. May 2010. ISSN 1088-9477. OCLC 34550461.
Working with Ben Green, he proved there are arbitrarily long arithmetic progressions of prime numbers—a result now known as the Green–Tao theorem.
- Jump up^ http://arxiv.org/pdf/math/0412006v2.pdf
- Jump up^ Green, Ben (2004), “The Cameron–Erdős conjecture”, The Bulletin of the London Mathematical Society 36 (6): 769–778, arXiv:math.NT/0304058,doi:10.1112/S0024609304003650, MR 2083752
- Jump up^ “News from 2007”. American Mathematical Society. AMS. 31 December 2007. Retrieved 2015-11-13.
The 2007 prize also recognizes Green for “his many outstanding results including his resolution of the Cameron-Erdős conjecture…”
- Jump up^http://archive.numdam.org/ARCHIVE/PMIHES/PMIHES_2003__98_/PMIHES_2003__98__1_0/PMIHES_2003__98__1_0.pdf
- Jump up^ “Kemnitz’ conjecture revisited”.
- Jump up^ http://www.ams.org/journals/jams/2004-17-01/S0894-0347-03-00440-5/S0894-0347-03-00440-5.pdf
- Jump up^ http://annals.math.princeton.edu/wp-content/uploads/annals-v158-n1-p04.pdf
- Jump up^ “The strong perfect graph theorem”.
- Jump up^ http://www.emis.de/journals/BAG/vol.43/no.1/b43h1haa.pdf
- Jump up^ Knight, R. W. (2002), The Vaught Conjecture: A Counterexample, manuscript
- Jump up^ http://www.ugr.es/~ritore/preprints/0406017.pdf
- Jump up^ Metsänkylä, Tauno (5 September 2003). “Catalan’s conjecture: another old diophantine problem solved” (PDF). Bulletin of the American Mathematical Society (American Mathematical Society) 41 (1): 43–57. ISSN 0273-0979.
The conjecture, which dates back to 1844, was recently proven by the Swiss mathematician Preda Mihăilescu.
- Jump up^ http://www.ams.org/journals/jams/2001-14-04/S0894-0347-01-00373-3/S0894-0347-01-00373-3.pdf
- Jump up^ http://junon.u-3mrs.fr/monniaux/AHLMT02.pdf
- Jump up^ http://arxiv.org/pdf/math/0102150v4.pdf
- Jump up^ Breuil, Christophe; Conrad, Brian; Diamond, Fred; Taylor, Richard (2001), “On the modularity of elliptic curves over Q: wild 3-adic exercises”, Journal of the American Mathematical Society 14 (4): 843–939, doi:10.1090/S0894-0347-01-00370-8, ISSN 0894-0347, MR 1839918
- Jump up^ http://www.ams.org/journals/mcom/2001-70-234/S0025-5718-00-01178-9/S0025-5718-00-01178-9.pdf
- Jump up^ http://intlpress.com/site/pub/files/_fulltext/journals/sdg/2002/0007/0001/SDG-2002-0007-0001-a001.pdf
- Jump up^ Croot, Ernest S., III (2000), Unit Fractions, Ph.D. thesis, University of Georgia, Athens. Croot, Ernest S., III (2003), “On a coloring conjecture about unit fractions”,Annals of Mathematics 157 (2): 545–556, arXiv:math.NT/0311421,doi:10.4007/annals.2003.157.545
- Jump up^ http://arxiv.org/pdf/math/9906042v2.pdf
- Jump up^ http://arxiv.org/pdf/math/9906212v2.pdf
- Jump up^ Ullmo, E. (1998), “Positivité et Discrétion des Points Algébriques des Courbes”, Annals of Mathematics 147 (1): 167–179, doi:10.2307/120987, Zbl 0934.14013
- Jump up^ Zhang, S.-W. (1998), “Equidistribution of small points on abelian varieties”, Annals of Mathematics 147 (1): 159–165, doi:10.2307/120986
- Jump up^ Lafforgue, Laurent (1998), “Chtoucas de Drinfeld et applications” [Drinfelʹd shtukas and applications], Documenta Mathematica (in French) II: 563–570,ISSN 1431-0635, MR 1648105
- Jump up^ http://arxiv.org/pdf/1501.02155.pdf
- Jump up^ http://arxiv.org/pdf/math/9811079v3.pdf
- Jump up^ Norio Iwase (1 November 1998). “Ganea’s Conjecture on Lusternik-Schnirelmann Category”. ResearchGate.
- Jump up^ Merel, Loïc (1996). “Bornes pour la torsion des courbes elliptiques sur les corps de nombres” [Bounds for the torsion of elliptic curves over number fields]. Inventiones Mathematicae (in French) 124 (1): 437–449. doi:10.1007/s002220050059. MR 1369424
- Jump up^https://www.researchgate.net/profile/Zhibo_Chen/publication/220188021_Harary’s_conjectures_on_integral_sum_graphs/links/5422b2490cf290c9e3aac7fe.pdf
- Jump up^ Wiles, Andrew (1995). “Modular elliptic curves and Fermat’s Last Theorem”(PDF). Annals of Mathematics (Annals of Mathematics) 141 (3): 443–551.doi:10.2307/2118559. JSTOR 2118559. OCLC 37032255.
- Jump up^ Taylor R, Wiles A (1995). “Ring theoretic properties of certain Hecke algebras”.Annals of Mathematics (Annals of Mathematics) 141 (3): 553–572.doi:10.2307/2118560. JSTOR 2118560. OCLC 37032255.
Further reading
Books discussing recently solved problems[dated info]
- Singh, Simon (2002). Fermat’s Last Theorem. Fourth Estate. ISBN 1-84115-791-0.
- O’Shea, Donal (2007). The Poincaré Conjecture. Penguin. ISBN 978-1-84614-012-9.
- Szpiro, George G. (2003). Kepler’s Conjecture. Wiley. ISBN 0-471-08601-0.
- Ronan, Mark (2006). Symmetry and the Monster. Oxford. ISBN 0-19-280722-6.
Books discussing unsolved problems
- Fan Chung; Graham, Ron (1999). Erdos on Graphs: His Legacy of Unsolved Problems. AK Peters. ISBN 1-56881-111-X.
- Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1994). Unsolved Problems in Geometry. Springer. ISBN 0-387-97506-3.
- Guy, Richard K. (2004). Unsolved Problems in Number Theory. Springer. ISBN 0-387-20860-7.
- Klee, Victor; Wagon, Stan (1996). Old and New Unsolved Problems in Plane Geometry and Number Theory. The Mathematical Association of America. ISBN 0-88385-315-9.
- Du Sautoy, Marcus (2003). The Music of the Primes: Searching to Solve the Greatest Mystery in Mathematics. Harper Collins. ISBN 0-06-093558-8.
- Derbyshire, John (2003). Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. Joseph Henry Press. ISBN 0-309-08549-7.
- Devlin, Keith (2006). The Millennium Problems – The Seven Greatest Unsolved* Mathematical Puzzles Of Our Time. Barnes & Noble. ISBN 978-0-7607-8659-8.
- Blondel, Vincent D.; Megrestski, Alexandre (2004). Unsolved problems in mathematical systems and control theory. Princeton University Press. ISBN 0-691-11748-9.
- Lizhen Ji, [various]; Yat-Sun Poon, Shing-Tung Yau (2013). Open Problems and Surveys of Contemporary Mathematics (volume 6 in the Surveys in Modern Mathematics series) (Surveys of Modern Mathematics). International Press of Boston. ISBN 1-571-46278-3.
- Waldschmidt, Michel (2004). “Open Diophantine Problems” (PDF). Moscow Mathematical Journal 4 (1): 245–305. ISSN 1609-3321. Zbl 1066.11030.
- Mazurov, V. D.; Khukhro, E. I. (1 Jun 2015). “Unsolved Problems in Group Theory. The Kourovka Notebook. No. 18 (English version)”. arXiv:1401.0300v6.
- Derbyshire, John (2003). Prime Obsession. The Joseph Henry Press. ISBN 0-309-08549-7.
External links
- 24 Unsolved Problems and Rewards for them
- List of links to unsolved problems in mathematics, prizes and research
- Open Problem Garden The collection of open problems in mathematics build on the principle of user editable (“wiki”) site
- AIM Problem Lists
- Unsolved Problem of the Week Archive. MathPro Press.
- Aizenman, Michael. “Open Problems in Mathematical Physics”.
- Ball, John M. “Some Open Problems in Elasticity” (PDF).
- Constantin, Peter. “Some open problems and research directions in the mathematical study of fluid dynamics” (PDF).
- Serre, Denis. “Five Open Problems in Compressible Mathematical Fluid Dynamics” (PDF).
- Unsolved Problems in Number Theory, Logic and Cryptography
- 200 open problems in graph theory
- The Open Problems Project (TOPP), discrete and computational geometry problems
- Kirby’s list of unsolved problems in low-dimensional topology
- Erdös’ Problems on Graphs
- A List of Approachable Open Problems in Knot Theory
- Unsolved Problems in Virtual Knot Theory and Combinatorial Knot Theory
- Open problems from the 12th International Conference on Fuzzy Set Theory and Its Applications
- List of open problems in inner model theory
- Open Problems in Mathematical Physics
- 15 Problems in Mathematical Physics
Unsolved Problems in Medicine
This article lists currently unsolved problems in medicine.
Problems or unknown causes for diseases
- Alzheimers Disease
- Acrocyanosis
- Bell’s Palsy
- Benign Fasciculation Syndrome
- Benign Paroxysmal Vertigo of Childhood
- Calciphylaxis
- Cardiac Syndrome X
- Cluster Headache
- Complex regional pain syndrome
- Copenhagen Disease
- Cronkhite-Canada Syndrome
- Dermatomyositis
- Cyclic vomiting syndrome
- Danubian endemic familial nephropathy
- Dialysis disequilibrium syndrome
- Exploding head syndrome
- Fibromyalgia
- Fields’ disease
- Floating-Harbor Syndrome
- Geographic tongue
- Granuloma annulare
- Idiopathic intracranial hypertension
- Irritable bowel syndrome
- Interstitial cystitis
- Kawasaki disease
- Mesoamerican nephropathy
- Mortimer’s disease
- Myofascial pain syndrome
- Nodding disease
- Sweating sickness
- Pigmented villonodular synovitis
- Pityriasis rosea
- Prurigo nodularis
- SAPHO syndrome
- Sarcoidosis
- Sjögren’s syndrome
- Spontaneous cerebrospinal fluid leak
- Stiff person syndrome
- Sudden infant death syndrome
- Synovial osteochondromatosis
- TEMPI syndrome
- Trigger finger
- Tropical sprue
- Villitis of unknown etiology
- Lymphedema
(Note: Current diseases being researched for cures are not on this list e.g. Cancer, due to usually using available knowledge of the causes and epidemiology to manage symptoms, having treatments already available for that ailment or find a cure through their based epidemiological vectors.)
Unsolved Problems in Neuroscience
There are yet unsolved problems in neuroscience, although some of these problems have evidence supporting a hypothesized solution, and the field is rapidly evolving. These problems include:
- Consciousness: What is the neural basis of subjective experience, cognition, wakefulness, alertness, arousal, and attention? Is there a “hard problem of consciousness“? If so, how is it solved? What, if any, is the function of consciousness?[1][2]
- Perception: How does the brain transfer sensory information into coherent, private percepts? What are the rules by which perception is organized? What are the features/objects that constitute our perceptual experience of internal and external events? How are the senses integrated? What is the relationship between subjective experience and the physical world?
- Learning and memory: Where do our memories get stored and how are they retrieved again? How can learning be improved? What is the difference betweenexplicit and implicit memories? What molecule is responsible for synaptic tagging?
- Neuroplasticity: How plastic is the mature brain?
- Development and evolution: How and why did the brain evolve? What are the molecular determinants of individual brain development?
- Free will, particularly the neuroscience of free will
- Sleep: What is the biological function of sleep? Why do we dream? What are the underlying brain mechanisms? What is its relation to anesthesia?
- Cognition and decisions: How and where does the brain evaluate reward value and effort (cost) to modulate behavior? How does previous experience alter perception and behavior? What are the genetic and environmental contributions to brain function?
- Language: How is it implemented neurally? What is the basis of semantic meaning?
- Diseases: What are the neural bases (causes) of mental diseases like psychotic disorders (e.g. mania, schizophrenia), Parkinson’s disease, Alzheimer’s disease, or addiction? Is it possible to recover loss of sensory or motor function?
- Movement: How can we move so controllably, even though the motor nerve impulses seem haphazard and unpredictable?[3]
- Computational theory of mind: What are the limits of understanding thinking as a form of computing?
- Computational neuroscience: How important is the precise timing of action potentials for information processing in the neocortex? Is there a canonical computation performed by cortical columns? How is information in the brain processed by the collective dynamics of large neuronal circuits? What level of simplification is suitable for a description of information processing in the brain? What is the neural code?
- How does general anesthetic work?
- Neural computation: What are all the different types of neuron and what do they do in the human brain?[4]
References
- Jump up^ Sejnowski, Terrence J.; Hemmen, J. L. van (2006). 23 problems in systems neuroscience (PDF). Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-514822-3.
- Jump up^ Tononi, G; Koch, C. (2015). “Consciousness: Here, there and everywhere?” (PDF). Philosophical Transactions of the Royal Society London B.
- Jump up^ University of Copenhagen (24 January 2007). “Thinking With The Spinal Cord?”. ScienceDaily. Retrieved 25 May 2016.
- Jump up^ A Database Of All Things Brainy
External links
- The Human Brain Project Homepage
- David Eagleman (August 2007). “10 Unsolved Mysteries of the Brain”. Discover Magazine.
- Dennett D (April 2001). “Are we explaining consciousness yet?”. Cognition 79 (1-2): 221–37. doi:10.1016/S0010-0277(00)00130-X. PMID 11164029.
Unsolved Problems in Philosophy
This is a list of some of the major unsolved problems in philosophy. Clearly, unsolved philosophical problems exist in the lay sense (e.g. “What is the meaning of life?“, “Where did we come from?“, “What is reality?“, etc.). However, professional philosophers generally accord serious philosophical problems specific names or questions, which indicate a particular method of attack or line of reasoning. As a result, broad and untenable topics become manageable. It would therefore be beyond the scope of this article to categorize “life” (and similar vague categories) as an unsolved philosophical problem.
Aesthetics
Essentialism
Main article: Essentialism
In art, essentialism is the idea that each medium has its own particular strengths and weaknesses, contingent on its mode of communication. A chase scene, for example, may be appropriate for motion pictures, but poorly realized in poetry, because the essential components of the poetic medium are ill suited to convey the information of a chase scene. This idea may be further refined, and it may be said that the haiku is a poor vehicle for describing a lover’s affection, as opposed to the sonnet. Essentialism is attractive to artists, because it not only delineates the role of art and media, but also prescribes a method for evaluating art (quality correlates to the degree of organic form). However, considerable criticism has been leveled at essentialism, which has been unable to formally define organic form or for that matter, medium. What, after all, is the medium of poetry? If it is language, how is this distinct from the medium of prose fiction? Is the distinction really a distinction in medium or genre? Questions about organic form, its definition, and its role in art remain controversial. Generally, working artists accept some form of the concept of organic form, whereas philosophers have tended to regard it as vague and irrelevant.
Art objects
This problem originally arose from the practice rather than theory of art. Marcel Duchamp, in the 20th century, challenged conventional notions of what “art” is, placing ordinary objects in galleries to prove that the context rather than content of an art piece determines what art is. In music, John Cage followed up on Duchamp’s ideas, asserting that the term “music” applied simply to the sounds heard within a fixed interval of time.
While it is easy to dismiss these assertions, further investigation[who?] shows that Duchamp and Cage are not so easily disproved. For example, if a pianist plays aChopin etude, but his finger slips missing one note, is it still the Chopin etude or a new piece of music entirely? Most people would agree that it is still a Chopin etude (albeit with a missing note), which brings into play the Sorites paradox, mentioned below. If one accepts that this is not a fundamentally changed work of music, however, is one implicitly agreeing with Cage that it is merely the duration and context of musical performance, rather than the precise content, which determines what music is? Hence, the question is what the criteria for art objects are and whether these criteria are entirely context-dependent.
Epistemology
Epistemological problems are concerned with the nature, scope and limitations of knowledge. Epistemology may also be described as the study of knowledge.
Gettier problem
Plato suggests, in his Theaetetus (210a) and Meno (97a–98b), that “knowledge” may be defined as justified true belief. For over two millennia, this definition of knowledge has been reinforced and accepted by subsequent philosophers. An item of information’s justifiability, truth, and belief have been seen as the necessary and sufficient conditions for knowledge.
In 1963, however, Edmund Gettier published an article in the periodical Analysis entitled “Is Justified True Belief Knowledge?”, offering instances of justified true belief that do not conform to the generally understood meaning of “knowledge.” Gettier’s examples hinged on instances of epistemic luck: cases where a person appears to have sound evidence for a proposition, and that proposition is in fact true, but the apparent evidence is not causally related to the proposition’s truth.
In response to Gettier’s article, numerous philosophers[who?] have offered modified criteria for “knowledge.” There is no general consensus to adopt any of the modified definitions yet proposed.
Problem of the criterion
Overlooking for a moment the complications posed by Gettier problems, philosophy has essentially continued to operate on the principle that knowledge is justified true belief. The obvious question that this definition entails is how one can know whether one’s justification is sound. One must therefore provide a justification for the justification. That justification itself requires justification, and the questioning continues interminably.
The conclusion is that no one can truly have knowledge of anything, since it is, due to this infinite regression, impossible to satisfy the justification element. In practice, this has caused little concern to philosophers, since the demarcation between a reasonably exhaustive investigation and superfluous investigation is usually clear.
Others argue for forms of coherentist systems, e.g. Susan Haack. Recent work by Peter D. Klein[1] views knowledge as essentially defeasible. Therefore, an infinite regress is unproblematic, since any known fact may be overthrown on sufficiently in depth investigation.
Molyneux problem
The Molyneux problem dates back to the following question posed by William Molyneux to John Locke in the 17th century: if a man born blind, and able to distinguish by touch between a cube and a globe, were made to see, could he now tell by sight which was the cube and which the globe, before he touched them? The problem raises fundamental issues in epistemology and the philosophy of mind, and was widely discussed after Locke included it in the second edition of hisEssay Concerning Human Understanding.[2]
A similar problem was also addressed earlier in the 12th century by Ibn Tufail (Abubacer), in his philosophical novel, Hayy ibn Yaqdhan (Philosophus Autodidactus). His version of the problem, however, dealt mainly with colors rather than shapes.[3][4]
Modern science may now have the tools necessary to test this problem in controlled environments. The resolution of this problem is in some sense provided by the study of human subjects who gain vision after extended congenital blindness. One such subject took approximately a year to recognize most household objects purely by sight.[citation needed] This indicates that this may no longer be an unsolved problem in philosophy.
Münchhausen trilemma
The Münchhausen trilemma, also called Agrippa‘s trilemma, purports that it is impossible to prove any certain truth even in fields such as logic and mathematics. According to this argument, the proof of any theory rests either on circular reasoning, infinite regress, or unproven axioms.
Qualia
See also: Distinguishing blue from green in language
The question hinges on whether color is a product of the mind or an inherent property of objects. While most philosophers will agree that color assignment corresponds to spectra of light frequencies, it is not at all clear whether the particular psychological phenomena of color are imposed on these visual signals by the mind, or whether such qualia are somehow naturally associated with their noumena. Another way to look at this question is to assume two people (“Fred” and “George” for the sake of convenience) see colors differently. That is, when Fred sees the sky, his mind interprets this light signal as blue. He calls the sky “blue.” However, when George sees the sky, his mind assigns green to that light frequency. If Fred were able to step into George’s mind, he would be amazed that George saw green skies. However, George has learned to associate the word “blue” with what his mind sees as green, and so he calls the sky “blue”, because for him the color green has the name “blue.” The question is whether blue must be blue for all people, or whether the perception of that particular color is assigned by the mind.
This extends to all areas of the physical reality, where the outside world we perceive is merely a representation of what is impressed upon the senses. The objects we see are in truth wave-emitting (or reflecting) objects which the brain shows to the conscious self in various forms and colors. Whether the colors and forms experienced perfectly match between person to person, may never be known. That people can communicate accurately shows that the order and proportionality in which experience is interpreted is generally reliable. Thus one’s reality is, at least, compatible to another person’s in terms of structure and ratio.
Ethics
Moral luck
The problem of moral luck is that some people are born into, live within, and experience circumstances that seem to change their moral culpability when all other factors remain the same.
For instance, a case of circumstantial moral luck: a poor person is born into a poor family, and has no other way to feed himself so he steals his food. Another person, born into a very wealthy family, does very little but has ample food and does not need to steal to get it. Should the poor person be more morally blameworthy than the rich person? After all, it is not his fault that he was born into such circumstances, but a matter of “luck”.
A related case is resultant moral luck. For instance, two persons behave in a morally culpable way, such as driving carelessly, but end up producing unequal amounts of harm: one strikes a pedestrian and kills him, while the other does not. That one driver caused a death and the other did not is no part of the drivers’ intentional actions; yet most observers would likely ascribe greater blame to the driver who killed (compare consequentialism and choice).
The fundamental question of moral luck is how our moral responsibility is changed by factors over which we have no control.
Moral knowledge
Are moral facts possible, what do they consist in, and how do we come to know them? Rightness and wrongness seem strange kinds of entities, and different from the usual properties of things in the world, such as wetness, being red, or solidity. Richmond Campbell[5] has outlined these kinds of issues in his encyclopedia article Moral Epistemology.
In particular, he considers three alternative explanations of moral facts as: theological, (supernatural, the commands of God); non-natural (based on intuitions); or simply natural properties (such as leading to pleasure or to happiness). There are cogent arguments against each of these alternative accounts, he claims, and there has not been any fourth alternative proposed. So the existence of moral knowledge and moral facts remains dubious and in need of further investigation. But moral knowledge supposedly already plays an important part in our everyday thinking, in our legal systems and criminal investigations.
Philosophy of mathematics
Mathematical objects
What are numbers, sets, groups, points, etc.? Are they real objects or are they simply relationships that necessarily exist in all structures? Although many disparate views exist regarding what a mathematical object is, the discussion may be roughly partitioned into two opposing schools of thought: platonism, which asserts that mathematical objects are real, and formalism, which asserts that mathematical objects are merely formal constructions. This dispute may be better understood when considering specific examples, such as the “continuum hypothesis“. The continuum hypothesis has been proven independent of the ZF axioms of set theory, so according to that system, the proposition can neither be proven true nor proven false. A formalist would therefore say that the continuum hypothesis is neither true nor false, unless you further refine the context of the question. A platonist, however, would assert that there either does or does not exist a transfinite set with acardinality less than the continuum but greater than any countable set.[citation needed] So, regardless of whether it has been proven unprovable, the platonist would argue that an answer nonetheless does exist.
Metaphysics
Sorites paradox
Otherwise known as the “paradox of the heap”, the question regards how one defines a “thing.” Is a bale of hay still a bale of hay if you remove one straw? If so, is it still a bale of hay if you remove another straw? If you continue this way, you will eventually deplete the entire bale of hay, and the question is: at what point is it no longer a bale of hay? While this may initially seem like a superficial problem, it penetrates to fundamental issues regarding how we define objects. This is similar toTheseus’ paradox and the Continuum fallacy.
Counterfactuals
A counterfactual is a statement that follows this form: “If Joseph Swan had not invented the modern incandescent light bulb, then someone else would have invented it anyway.” People use counterfactuals every day; however, its analysis is not so clear. Swan, after all, did invent the modern incandescent light bulb, so how can the statement be true, if it is impossible to examine its correspondence to reality? (See correspondence theory of truth.) Similar statements have the form, “If you don’t eat your meat, then you can’t have any pudding.” This is another clear if-then statement, which is not verifiable (assuming the addressee did eat his/her meat). Two proposed analyses have resulted from this question. First, some philosophers assert that background information is assumed when stating and interpreting counterfactual conditionals. In the case of the Swan statement, certain trends in the history of technology, the utility of artificial light, and the discovery of electricity may all provide evidence for a logically sound argument. However, other philosophers assert that a modal “possible world” theory offers a more accurate description of counterfactual conditionals. According to this analysis, in the Swan example one would consider the closest possible world to the real world in whichSwan did not create the modern incandescent light bulb. When a counterfactual is used as an argument to justify an illegal act, it is known as the dirty hands argument. For example, “if I didn’t sell him drugs then someone else would have, and those drugs might not have been cut or more harmful.”
Material implication
People have a pretty clear idea what if-then means. In formal logic however, material implication defines if-then, which is not consistent with the common understanding of conditionals. In formal logic, the statement “If today is Saturday, then 1+1=2” is true. However, ‘1+1=2’ is true regardless of the content of the antecedent; a causal or meaningful relation is not required. The statement as a whole must be true, because 1+1=2 cannot be false. (If it could, then on a given Saturday, so could the statement). Formal logic has shown itself extremely useful in formalizing argumentation, philosophical reasoning, and mathematics. The discrepancy between material implication and the general conception of conditionals however is a topic of intense investigation: whether it is an inadequacy in formal logic, an ambiguity of ordinary language, or as championed by H.P. Grice, that no discrepancy exists.
Philosophy of mind
Mind–body problem
The mind–body problem is the problem of determining the relationship between the human body and the human mind. Philosophical positions on this question are generally predicated on either a reduction of one to the other, or a belief in the discrete coexistence of both. This problem is usually exemplified by Descartes, who championed a dualistic picture. The problem therein is to establish how the mind and body communicate in a dualistic framework. Neurobiology and emergencehave further complicated the problem by allowing the material functions of the mind to be a representation of some further aspect emerging from the mechanistic properties of the brain. The brain essentially stops generating conscious thought during deep sleep; the ability to restore such a pattern remains a mystery to science and is a subject of current research (see also neurophilosophy).
Cognition and AI
This problem actually defines a field, however its pursuits are specific and easily stated. Firstly, what are the criteria for intelligence? What are the necessary components for defining consciousness? Secondly, how can an outside observer test for these criteria? The “Turing Test” is often cited as a prototypical test of consciousness, although it is almost universally regarded as insufficient. It involves a conversation between a sentient being and a machine, and if the being can’t tell he is talking to a machine, it is considered intelligent. A well trained machine, however, could theoretically “parrot” its way through the test. This raises the corollary question of whether it is possible to artificially create consciousness (usually in the context of computers or machines), and of how to tell a well trained mimic from a sentient entity.
Important thought in this area includes most notably: John Searle‘s Chinese Room, Hubert Dreyfus‘ non-cognitivist critique, as well as Hilary Putnam‘s work onFunctionalism.
A related field is the ethics of artificial intelligence, which addresses such problems as the existence of moral personhood of AIs, the possibility of moral obligationsto AIs (for instance, the right of a possibly sentient computer system to not be turned off), and the question of making AIs that behave ethically towards humans and others.
Hard problem of consciousness
The hard problem of consciousness is the question of what consciousness is and why we have consciousness as opposed to being philosophical zombies. The adjective “hard” is to contrast with the “easy” consciousness problems, which seek to explain the mechanisms of consciousness (“why” versus “how,” or final causeversus efficient cause). The hard problem of consciousness is questioning whether all beings undergo an experience of consciousness rather than questioning the neurological makeup of beings.
Philosophy of science
Problem of induction
Intuitively, it seems to be the case that we know certain things with absolute, complete, utter, unshakable certainty. For example, if you travel to the Arctic and touch an iceberg, you know that it would feel cold. These things that we know from experience are known through induction. The problem of induction in short; (1) any inductive statement (like the sun will rise tomorrow) can only be deductively shown if one assumes that nature is uniform. (2) the only way to show that nature is uniform is by using induction. Thus induction cannot be justified deductively.
Demarcation problem
‘The problem of demarcation’ is an expression introduced by Karl Popper to refer to ‘the problem of finding a criterion which would enable us to distinguish between the empirical sciences on the one hand, and mathematics and logic as well as “metaphysical” systems on the other’. Popper attributes this problem to Kant. Although Popper mentions mathematics and logic, other writers focus on distinguishing science from metaphysics and pseudo-science.
Some, including Popper, raise the problem because of an intellectual desire to clarify this distinction.[citation needed] Logical positivists had, in addition, a social and intellectual agenda to discredit non-scientific disciplines.[citation needed]
Realism
Does a world independent of human beliefs and representations exist? Is such a world empirically accessible, or would such a world be forever beyond the bounds of human sense and hence unknowable? Can human activity and agency change the objective structure of the world? These questions continue to receive much attention in the philosophy of science. A clear “yes” to the first question is a hallmark of the scientific realism perspective. Philosophers such as Bas van Fraassenhave important and interesting answers to the second question. In addition to the realism vs. empiricism axis of debate, there is a realism vs. social constructivismaxis which heats many academic passions. With respect to the third question, Paul Boghossian‘s “Fear of Knowledge: Against Relativism and Constructivism”. Oxford University Press. 2006. is a powerful critique of social constructivism, for instance. Ian Hacking’s The Social Construction of What? (Harvard UP, 2000) constitutes a more moderate critique of constructivism, which usefully disambiguates confusing polysemy of the term “constructivism.”
See also
References
- Jump up^ Klein, P. D., “Human Knowledge and the Infinite Progress of Reasoning,” Philosophical Studies, 134. 1, 2007, 1-17.
- Jump up^ Locke, John. An Essay Concerning Human Understanding, Book 2, Chapter 9.
“I shall here insert a problem of that very ingenious and studious promoter of real knowledge, the learned and worthy Mr. Molyneux, which he was pleased to send me in a letter some months since; and it is this:—”Suppose a man born blind, and now adult, and taught by his touch to distinguish between a cube and a sphere of the same metal, and nighly of the same bigness, so as to tell, when he felt one and the other, which is the cube, which the sphere. Suppose then the cube and sphere placed on a table, and the blind man be made to see: quaere, whether by his sight, before he touched them, he could now distinguish and tell which is the globe, which the cube?” To which the acute and judicious proposer answers, “Not. For, though he has obtained the experience of how a globe, how a cube affects his touch, yet he has not yet obtained the experience, that what affects his touch so or so, must affect his sight so or so; or that a protuberant angle in the cube, that pressed his hand unequally, shall appear to his eye as it does in the cube.”—I agree with this thinking gentleman, whom I am proud to call my friend, in his answer to this problem; and am of opinion that the blind man, at first sight, would not be able with certainty to say which was the globe, which the cube, whilst he only saw them; though he could unerringly name them by his touch, and certainly distinguish them by the difference of their figures felt. This I have set down, and leave with my reader, as an occasion for him to consider how much he may be beholden to experience, improvement, and acquired notions, where he thinks he had not the least use of, or help from them. And the rather, because this observing gentleman further adds, that “having, upon the occasion of my book, proposed this to divers very ingenious men, he hardly ever met with one that at first gave the answer to it which he thinks true, till by hearing his reasons they were convinced.”
- Jump up^ Muhammad ibn Abd al-Malik Ibn Tufayl and Léon Gauthier (1981), Risalat Hayy ibn Yaqzan, p. 5, Editions de la Méditerranée.
“If you want a comparison that will make you clearly grasp the difference between the perception, such as it is understood by that sect [the Sufis] and the perception as others understand it, imagine a person born blind, endowed however with a happy natural temperament, with a lively and firm intelligence, a surememory, a straight sprite, who grew up from the time he was an infant in a city where he never stopped learning, by means of the senses he did dispose of, to know the inhabitants individually, the numerous species of beings, living as well as non-living, there, the streets and sidestreets, the houses, the steps, in such a manner as to be able to cross the city without a guide, and to recognize immediately those he met; the colors alone would not be known to him except by the names they bore, and by certain definitions that designated them. Suppose that he had arrived at this point and suddenly, his eyes were opened, he recovered his view, and he crosses the entire city, making a tour of it. He would find no object different from the idea he had made of it; he would encounter nothing he didn’t recognize, he would find the colors conformable to the descriptions of them that had been given to him; and in this there would only be two new important things for him, one the consequence of the other: a clarity, a greater brightness, and a great voluptuousness.”
- Jump up^ Lobel, Diana. A Sufi-Jewish Dialogue: Philosophy and Mysticism in Baḥya Ibn Paqūda’s Duties of the Heart, University of Pennsylvania Press, 2006, p.24. ISBN 0-8122-3953-9
- Jump up^ Campbell, Richmond, “Moral Epistemology”, The Stanford Encyclopedia of Philosophy (Spring 2014 Edition), Edward N. Zalta (ed.)
Unsolved Problems in Physics
Some of the major unsolved problems in physics are theoretical, meaning that existing theories seem incapable of explaining a certain observed phenomenon or experimental result. The others are experimental, meaning that there is a difficulty in creating an experiment to test a proposed theory or investigate a phenomenon in greater detail.
Unsolved problems by subfield
The following is a list of unsolved problems grouped into broad area of physics.[1]
General physics/quantum physics
- Entropy (arrow of time)
- Why did the universe have such low entropy in the past, resulting in the distinction between past and future and the second law of thermodynamics?[2] Why areCP violations observed in certain weak force decays, but not elsewhere? Are CP violations somehow a product of the Second Law of Thermodynamics, or are they a separate arrow of time? Are there exceptions to the principle of causality? Is there a single possible past? Is the present moment physically distinct from the past and future or is it merely an emergent property of consciousness? Why does time have a direction? What links the quantum arrow of time to the thermodynamic arrow?
- Interpretation of quantum mechanics
- How does the quantum description of reality, which includes elements such as the superposition of states and wavefunction collapse or quantum decoherence, give rise to the reality we perceive? Another way of stating this question regards the measurement problem: What constitutes a “measurement” which causes the wave function to collapse into a definite state? Unlike classical physical processes, some quantum mechanical processes (such as quantum teleportationarising from quantum entanglement) cannot be simultaneously “local”, “causal”, and “real”, but it is not obvious which of these properties must be sacrificed or if an attempt to describe quantum mechanical processes in these senses is a category error such that a proper understanding of quantum mechanics would render the question meaningless.
- Grand Unification Theory (“Theory of everything“)
- Is there a theory which explains the values of all fundamental physical constants?[2] Is the theory string theory? Is there a theory which explains why the gauge groups of the standard model are as they are, why observed spacetime has 3 spatial dimensions and 1 temporal dimension, and why all laws of physics are as they are? Do “fundamental physical constants” vary over time? Are any of the particles in the standard model of particle physics actually composite particles too tightly bound to observe as such at current experimental energies? Are there fundamental particles that have not yet been observed, and, if so, which ones are they and what are their properties? Are there unobserved fundamental forces implied by a theory that explains other unsolved problems in physics?
- Yang–Mills theory
- Given an arbitrary compact gauge group, does a non-trivial quantum Yang–Mills theory with a finite mass gap exist? This problem is also listed as one of theMillennium Prize Problems in mathematics.
- Physical information
- Are there physical phenomena, such as wave function collapse or black holes, which irrevocably destroy information about their prior states? How is quantum information stored as a state of a quantum system?
- Dimensionless physical constant
- At the present time, the values of the dimensionless physical constants cannot be calculated; they are determined only by physical measurement.[3][4] What is the minimum number of dimensionless physical constants from which all other dimensionless physical constants can be derived? Are dimensionful physical constants necessary at all?
- Fine-tuned Universe
- What explains why the fundamental physical constants are set in the narrow range that is necessary to support carbon-based life?
Cosmology and general relativity
- Problem of time
- How can time be reconciled with general relativity?
- Cosmic inflation
- Is the theory of cosmic inflation correct, and, if so, what are the details of this epoch? What is the hypothetical inflaton field giving rise to inflation? If inflation happened at one point, is it self-sustaining through inflation of quantum-mechanical fluctuations, and thus ongoing in some extremely distant place?[5]
- Horizon problem
- Why is the distant universe so homogeneous when the Big Bang theory seems to predict larger measurable anisotropies of the night sky than those observed? Cosmological inflation is generally accepted as the solution, but are other possible explanations such as a variable speed of light more appropriate?[6]
- Future of the universe
- Is the universe heading towards a Big Freeze, a Big Rip, a Big Crunch, or a Big Bounce? Or is it part of an infinitely recurring cyclic model?
- Baryon asymmetry
- Why is there far more matter than antimatter in the observable universe?
- Cosmological constant problem
- Why does the zero-point energy of the vacuum not cause a large cosmological constant? What cancels it out?[7]
- Dark matter
- What is the identity of dark matter?[6] Is it a particle? Is it the lightest superpartner (LSP)? Do the phenomena attributed to dark matter point not to some form of matter but actually to an extension of gravity?
- Dark energy
- What is the cause of the observed accelerated expansion (de Sitter phase) of the Universe? Why is the energy density of the dark energy component of the same magnitude as the density of matter at present when the two evolve quite differently over time; could it be simply that we are observing at exactly the right time? Is dark energy a pure cosmological constant or are models of quintessence such as phantom energy applicable?
- Dark flow
- Is a non-spherically symmetric gravitational pull from outside the observable Universe responsible for some of the observed motion of large objects such as galactic clusters in the universe?
- Ecliptic alignment of CMB anisotropy
- Some large features of the microwave sky at distances of over 13 billion light years appear to be aligned with both the motion and orientation of the solar system. Is this due to systematic errors in processing, contamination of results by local effects, or an unexplained violation of the Copernican principle?
- Shape of the Universe
- What is the 3-manifold of comoving space, i.e. of a comoving spatial section of the Universe, informally called the “shape” of the Universe? Neither the curvature nor the topology is presently known, though the curvature is known to be “close” to zero on observable scales. The cosmic inflation hypothesis suggests that the shape of the Universe may be unmeasurable, but, since 2003, Jean-Pierre Luminet, et al., and other groups have suggested that the shape of the Universe may be the Poincaré dodecahedral space. Is the shape unmeasurable; the Poincaré space; or another 3-manifold?
Quantum gravity
- Vacuum catastrophe
- Why does the predicted mass of the quantum vacuum have little effect on the expansion of the universe?
- Quantum gravity
- Can quantum mechanics and general relativity be realized as a fully consistent theory (perhaps as a quantum field theory)?[8] Is spacetime fundamentally continuous or discrete? Would a consistent theory involve a force mediated by a hypothetical graviton, or be a product of a discrete structure of spacetime itself (as in loop quantum gravity)? Are there deviations from the predictions of general relativity at very small or very large scales or in other extreme circumstances that flow from a quantum gravity theory?
- Black holes, black hole information paradox, and black hole radiation
- Do black holes produce thermal radiation, as expected on theoretical grounds? Does this radiation contain information about their inner structure, as suggested by gauge–gravity duality, or not, as implied by Hawking‘s original calculation? If not, and black holes can evaporate away, what happens to the information stored in them (since quantum mechanics does not provide for the destruction of information)? Or does the radiation stop at some point leaving black hole remnants? Is there another way to probe their internal structure somehow, if such a structure even exists?
- Extra dimensions
- Does nature have more than four spacetime dimensions? If so, what is their size? Are dimensions a fundamental property of the universe or an emergent result of other physical laws? Can we experimentally observe evidence of higher spatial dimensions?
- The cosmic censorship hypothesis and the chronology protection conjecture
- Can singularities not hidden behind an event horizon, known as “naked singularities“, arise from realistic initial conditions, or is it possible to prove some version of the “cosmic censorship hypothesis” of Roger Penrose which proposes that this is impossible?[9] Similarly, will the closed timelike curves which arise in some solutions to the equations of general relativity (and which imply the possibility of backwards time travel) be ruled out by a theory of quantum gravity which unites general relativity with quantum mechanics, as suggested by the “chronology protection conjecture” of Stephen Hawking?
- Locality
- Are there non-local phenomena in quantum physics? If they exist, are non-local phenomena limited to the entanglement revealed in the violations of the Bell inequalities, or can information and conserved quantities also move in a non-local way? Under what circumstances are non-local phenomena observed? What does the existence or absence of non-local phenomena imply about the fundamental structure of spacetime? How does this relate to quantum entanglement? How does this elucidate the proper interpretation of the fundamental nature of quantum physics?
High-energy physics/particle physics
- Higgs mechanism
- Are the branching ratios of the Higgs boson decays consistent with the standard model? Is there only one type of Higgs boson?
- Hierarchy problem
- Why is gravity such a weak force? It becomes strong for particles only at the Planck scale, around 1019 GeV, much above the electroweak scale (100 GeV, the energy scale dominating physics at low energies). Why are these scales so different from each other? What prevents quantities at the electroweak scale, such as the Higgs boson mass, from getting quantum corrections on the order of the Planck scale? Is the solution supersymmetry, extra dimensions, or just anthropicfine-tuning?
- Magnetic monopoles
- Did particles that carry “magnetic charge” exist in some past, higher-energy epoch? If so, do any remain today? (Paul Dirac showed the existence of some types of magnetic monopoles would explain charge quantization.)[10]
- Proton decay and spin crisis
- Is the proton fundamentally stable? Or does it decay with a finite lifetime as predicted by some extensions to the standard model?[11] How do the quarks and gluons carry the spin of protons?[12]
- Supersymmetry
- Is spacetime supersymmetry realized at TeV scale? If so, what is the mechanism of supersymmetry breaking? Does supersymmetry stabilize the electroweak scale, preventing high quantum corrections? Does the lightest supersymmetric particle (LSP or Lightest Supersymmetric Particle) comprise dark matter?
- Generations of matter
- Why are there three generations of quarks and leptons? Is there a theory that can explain the masses of particular quarks and leptons in particular generations from first principles (a theory of Yukawa couplings)?[13]
- Neutrino mass
- What is the mass of neutrinos, whether they follow Dirac or Majorana statistics? Is mass hierarchy normal or inverted? Is the CP violating phase 0?[14][15][16]
- Color confinement
- Why has there never been measured a free quark or gluon, but only objects that are built out of them, such as mesons and baryons? How does this phenomenon emerge from QCD?
- Strong CP problem and axions
- Why is the strong nuclear interaction invariant to parity and charge conjugation? Is Peccei–Quinn theory the solution to this problem?
- Anomalous magnetic dipole moment
- Why is the experimentally measured value of the muon‘s anomalous magnetic dipole moment (“muon g−2”) significantly different from the theoretically predicted value of that physical constant?[17]
- Proton size puzzle
- What is the electric charge radius of the proton? How does it differ from gluonic charge?
- Pentaquarks and other exotic hadrons
- What combinations of quarks are possible? Why were pentaquarks so difficult to discover?[18] Are they a tightly-bound system of five elementary particles, or a more weakly-bound pairing of a baryon and a meson?[19]
Astronomy and astrophysics
Relativistic jet. The environment around theAGN where the relativistic plasma is collimated into jets which escape along the pole of thesupermassive black hole.
- Astrophysical jet
- Why do the accretion discs surrounding certain astronomical objects, such as the nuclei of active galaxies, emitrelativistic jets along their polar axes?[20] Why are there quasi-periodic oscillations in many accretion discs?[21]Why does the period of these oscillations scale as the inverse of the mass of the central object?[22] Why are there sometimes overtones, and why do these appear at different frequency ratios in different objects?[23]
- Coronal heating problem
- Why is the Sun’s corona (atmosphere layer) so much hotter than the Sun’s surface? Why is the magnetic reconnection effect many orders of magnitude faster than predicted by standard models?
- Diffuse interstellar bands
- What is responsible for the numerous interstellar absorption lines detected in astronomical spectra? Are they molecular in origin, and if so which molecules are responsible for them? How do they form?
- Supermassive black holes
- What is the origin of the M-sigma relation between supermassive black hole mass and galaxy velocity dispersion?[24] How did the most distant quasars grow their supermassive black holes up to 1010 solar masses so early in the history of the Universe?
- Kuiper cliff
- Why does the number of objects in the Solar System’s Kuiper belt fall off rapidly and unexpectedly beyond a radius of 50 astronomical units?
- Flyby anomaly
- Why is the observed energy of satellites flying by Earth sometimes different by a minute amount from the value predicted by theory?
- Galaxy rotation problem
- Is dark matter responsible for differences in observed and theoretical speed of stars revolving around the center of galaxies, or is it something else?
- Supernovae
- What is the exact mechanism by which an implosion of a dying star becomes an explosion?
- Ultra-high-energy cosmic ray
- [6] Why is it that some cosmic rays appear to possess energies that are impossibly high,given that there are no sufficiently energetic cosmic ray sources near the Earth? Why is it that (apparently) some cosmic rays emitted by distant sources have energies above the Greisen–Zatsepin–Kuzmin limit?[2][6]
- Rotation rate of Saturn
- Why does the magnetosphere of Saturn exhibit a (slowly changing) periodicity close to that at which the planet’s clouds rotate? What is the true rotation rate of Saturn’s deep interior?[25]
- Origin of magnetar magnetic field
- What is the origin of magnetar magnetic field?
- Large-scale anisotropy
- Is the Universe at very large scales anisotropic, making the cosmological principle an invalid assumption? The number count and intensity dipole anisotropy in radio, NRAO VLA Sky Survey (NVSS) catalogue[26] is inconsistent with the local motion as derived from cosmic microwave background[27][28] and indicate an intrinsic dipole anisotropy. The same NVSS radio data also shows an intrinsic dipole in polarization density and degree of polarization[29] in the same direction as in number count and intensity. There are other several observation revealing large-scale anisotropy. The optical polarization from quasars shows polarization alignment over a very large scale of Gpc.[30][31][32] The cosmic-microwave-background data shows several features of anisotropy,[33][34][35][36] which are not consistent with the Big Bang model.
- Space roar
- Why is space roar six times louder than expected? What is the source of space roar?
- Age–metallicity relation in the Galactic disk
- Is there a universal age–metallicity relation (AMR) in the Galactic disk (both “thin” and “thick” parts of the disk)? Although in the local (primarily thin) disk of theMilky Way there is no evidence of a strong AMR,[37] a sample of 229 nearby “thick” disk stars has been used to investigate the existence of an age–metallicity relation in the Galactic thick disk, and indicate that there is an age–metallicity relation present in the thick disk.[38][39] Stellar ages from asteroseismology confirm the lack of any strong age-metallicity relation in the Galactic disc.[40]
- The lithium problem
- Why is there a discrepancy between the amount of lithium-7 predicted to be produced in Big Bang nucleosynthesis and the amount observed in very old stars?[41]
- Solar wind interaction with comets
- In 2007 the Ulysses spacecraft passed through the tail of comet C/2006 P1 (McNaught) and found surprising results concerning the interaction of the solar wind with the tail.
- Ultraluminous pulsar
- The ultraluminous X-ray source M82 X-2 was thought to be a black hole, but in October 2014 data from NASA’s space-based X-ray telescope NuStar indicated that M82 X-2 is a pulsar many times brighter than the Eddington limit.
- The injection problem
- Fermi acceleration is thought to be the primary mechanism that accelerates astrophysical particles to high energy. However, it is unclear what mechanism causes those particles to initially have energies high enough for Fermi acceleration to work on them.[42]
- Fast radio bursts
- Transient radio pulses lasting only a few milliseconds, from emission regions thought to be no larger than a few hundred kilometers, and estimated to occur several hundred times a day. While several theories have been proposed, there is no generally accepted explanation for them. They may come from cosmological distances, but there is no consensus on this, either.[citation needed]
- Nature of KIC 8462852
- What is the origin of unusual luminosity changes of this star?
- Fermi paradox
- Do extraterrestrial civilizations exist? If so, why we do not see them?
- Nature of Wow! signal
- Was that a real signal and, if so, what is the origin of it?[43]
Nuclear physics
The “island of stability” in the proton vs. neutron number plot for heavy nuclei.
- Quantum chromodynamics
- What are the phases of strongly interacting matter, and what roles do they play in the evolution of cosmos? What is the detailed partonic structure of the nucleons? What does QCD predict for the properties of strongly interacting matter? What determines the key features of QCD, and what is their relation to the nature of gravity and spacetime? Doglueballs exist? Do gluons acquire mass dynamically despite having a zero rest mass, within hadrons? Does QCD truly lack CP-violations? Do gluons saturate[disambiguation needed] when their occupation number is large? Do gluons form a dense system called Color Glass Condensate? What are the signatures and evidences for the Balitsky-Fadin-Kuarev-Lipatov, Balitsky-Kovchegov, Catani-Ciafaloni-Fiorani-Marchesini evolution equations?
- Nuclei and nuclear astrophysics
- What is the nature of the nuclear force that binds protons and neutrons into stable nuclei and rare isotopes? What is the origin of simple patterns[which?] in complex nuclei? What is the nature of exotic excitations in nuclei at the frontiers of stability and their role in stellar processes? What is the nature of neutron starsand dense nuclear matter? What is the origin of the elements in the cosmos? What are the nuclear reactions that drive stars and stellar explosions?
- Plasma physics and fusion power
- Fusion energy may potentially provide power from abundant resource (e.g. hydrogen) without the type of radioactive waste that fission energy currently produces. However, can ionized gases (plasma) be confined long enough and at a high enough temperature to create fusion power? What is the physical mechanism of the transition from Low to High confinement scenarios?[44]
Atomic, molecular and optical physics
- Abraham–Minkowski controversy
- What is the momentum of photons in optical media?
Condensed matter physics
- High-temperature superconductors
- What is the mechanism that causes certain materials to exhibit superconductivity at temperatures much higher than around 25kelvin? Is it possible to make a material that is a superconductor at room temperature?[2]
- Amorphous solids
- What is the nature of the glass transition between a fluid or regular solid and a glassy phase? What are the physical processes giving rise to the general properties of glasses and the glass transition?[45][46]
- Cryogenic electron emission
- Why does the electron emission in the absence of light increase as the temperature of a photomultiplier is decreased?[47][48]
- Sonoluminescence
- What causes the emission of short bursts of light from imploding bubbles in a liquid when excited by sound?[49][50]
- Turbulence
- Is it possible to make a theoretical model to describe the statistics of a turbulent flow (in particular, its internal structures)?[2] Also, under what conditions do smooth solutions to the Navier–Stokes equations exist? This problem is also listed as one of the Millennium Prize Problems in mathematics.
- Alfvénic turbulence
- In the solar wind and the turbulence in solar flares, coronal mass ejections, and magnetospheric substorms are major unsolved problems in space plasma physics.[51]
- Topological order
- Is topological order stable at non-zero temperature? Equivalently, is it possible to have three-dimensional self-correcting quantum memory?[52]
- Fractional Hall effect
- What mechanism explains the existence of the
 state in the fractional quantum Hall effect? Does it describe quasiparticles with non-Abelian fractional statistics?[citation needed]
state in the fractional quantum Hall effect? Does it describe quasiparticles with non-Abelian fractional statistics?[citation needed] - Bose–Einstein condensation
- How do we rigorously prove the existence of Bose–Einstein condensates for general interacting systems?[53]
- Liquid crystals
- Can the nematic to smectic (A) phase transition in liquid crystal states be characterized as a universal phase transition?[54][55]
- Semiconductor nanocrystals
- What is the cause of the nonparabolicity of the energy-size dependence for the lowest optical absorption transition of quantum dots?[56]
- Electronic band structure
- Why can band gaps not be calculated accurately?
Biophysics
- Stochasticity and robustness to noise in gene expression
- How do genes govern our body, withstanding different external pressures and internal stochasticity? Certain models exist for genetic processes, but we are far from understanding the whole picture, in particular indevelopment where gene expression must be tightly regulated.
- Quantitative study of the immune system
- What are the quantitative properties of immune responses? What are the basic building blocks of immune system networks? What roles are played by stochasticity?
- Homochirality
- What is the origin of the preponderance of specific enantiomers in biochemical systems?
Problems solved in recent decades
- Existence of gravitational wave (1916-2016)
- On 11 February 2016, the Advanced LIGO team announced that they had directly detected gravitational waves from a pair of black holes merging,[57][58][59]which was also the first detection of a stellar binary black hole.
- Perform a loophole-free Bell test experiment (1970[60]-2015)
- In October 2015, scientists from the Kavli Institute of Nanoscience reported that the quantum nonlocality phenomenon is supported at the 96% confidence level based on a “loophole-free Bell test” study.[61][62] These results were confirmed by two studies with statistical significance over 5 standard deviations which were published in December 2015.[63][64]
- Existence of pentaquarks (1964-2015)
- In July 2015, the LHCb collaboration at CERN identified pentaquarks in the Λ0
b→J/ψK−
p channel, which represents the decay of the bottom lambda baryon (Λ0
b)into a J/ψ meson (J/ψ), a kaon (K−
) and a proton (p). The results showed that sometimes, instead of decaying directly into mesons and baryons, the Λ0
b decayed via intermediate pentaquark states. The two states, named P+
c(4380) and P+
c(4450), had individual statistical significances of 9 σ and 12 σ, respectively, and a combined significance of 15 σ — enough to claim a formal discovery. The two pentaquark states were both observed decaying strongly to J/ψp, hence must have a valence quark content of two up quarks, a down quark, a charm quark, and an anti-charm quark (uudcc), making them charmonium-pentaquarks.[65] - Photon underproduction crisis (2014-2015)
- This problem was resolved by Khaire and Srianand.[66] They show that a factor 2 to 5 times large metagalactic photoionization rate can be easily obtained using updated quasar and galaxy observations. Recent observations of quasars indicate that the quasar contribution to ultraviolet photons is factor 2 large as compared to previous estimates. The revised galaxy contribution is also factor 3 higher. This together solves the crisis.
- Existence of ball lightning (1638[67]-2014)
- In January 2014, scientists from Northwest Normal University in Lanzhou, China, published the results of recordings made in July 2012 of the optical spectrum of what was thought to be natural ball lightning made during the study of ordinary cloud–ground lightning on China’s Qinghai Plateau.[68][69] At a distance of 900 m (3,000 ft), a total of 1.3 seconds of digital video of the ball lightning and its spectrum was made, from the formation of the ball lightning after the ordinary lightning struck the ground, up to the optical decay of the phenomenon. The recorded ball lightning is believed to be vaporized soil elements that then rapidly oxidizes in the atmosphere. The nature of the true theory is still not clear.[69]
- Higgs boson and electroweak symmetry breaking (1963[70]-2012)
- The mechanism responsible for breaking the electroweak gauge symmetry, giving mass to the W and Z bosons, was solved with the discovery of the Higgs boson of the Standard Model, with the expected couplings to the weak bosons. No evidence of a strong dynamics solution, as proposed by technicolor, has been observed.
- Hipparcos anomaly (1997[71]-2012)
- The actual distance to the Pleiades – the High Precision Parallax Collecting Satellite (Hipparcos) measured the parallax of the Pleiades and determined a distance of 385 light years. This was significantly different from other measurements made by means of actual to apparent brightness measurement or absolute magnitude. The anomaly was due to the use of a weighted mean when there is a correlation between distances and distance errors for stars in clusters. It is resolved by using an unweighted mean. There is no systematic bias in the Hipparcos data when it comes to star clusters.[72]
- Faster-than-light neutrino anomaly (2011-2012)
- In 2011, the OPERA experiment mistakenly observed neutrinos appearing to travel faster than light. On July 12, 2012 OPERA updated their paper by including the new sources of errors in their calculations. They found agreement of neutrino speed with the speed of light.[73]
- Pioneer anomaly (1980-2012)
- There was a deviation in the predicted accelerations of the Pioneer spacecraft as they left the Solar System.[2][6] It is believed that this is a result of previously unaccounted-for thermal recoil force.[74][75]
- Long-duration gamma ray bursts (1993[76]-2003)
- Long-duration bursts are associated with the deaths of massive stars in a specific kind of supernova-like event commonly referred to as a collapsar. However, there are also long-duration GRBs that show evidence against an associated supernova, such as the Swift event GRB 060614.
- Solar neutrino problem (1968[77]-2001)
- Solved by a new understanding of neutrino physics, requiring a modification of the Standard Model of particle physics—specifically, neutrino oscillation.
- Create Bose–Einstein condensate (1924[78]-1995)
- Composite bosons in the form of dilute atomic vapors were cooled to quantum degeneracy using the techniques of laser cooling and evaporative cooling.
- Cosmic age problem (1920s-1990s)
- The estimated age of the universe was around 3 to 8 billion years younger than estimates of the ages of the oldest stars in the Milky Way. Better estimates for the distances to the stars, and the recognition of the accelerating expansion of the universe, reconciled the age estimates.
- Nature of quasars (1950s-1980s)
- The nature of quasars was not understood for decades.[79] They are now accepted as a type of active galaxy where the enormous energy output results from matter falling into a massive black hole in the center of the galaxy.[80]
See also
References
- Jump up^ Ginzburg, Vitaly L. (2001). The physics of a lifetime : reflections on the problems and personalities of 20th century physics. Berlin: Springer. pp. 3–200.ISBN 9783540675341.
- ^ Jump up to:a b c d e f Baez, John C. (March 2006). “Open Questions in Physics”. Usenet Physics FAQ. University of California, Riverside: Department of Mathematics. Retrieved March 7, 2011.
- Jump up^ “Alcohol constrains physical constant in the early universe”. Phys Org. December 13, 2012. Retrieved 25 March 2015.
- Jump up^ Bagdonaite, J.; Jansen, P.; Henkel, C.; Bethlem, H. L.; Menten, K. M.; Ubachs, W. (13 December 2012). “A Stringent Limit on a Drifting Proton-to-Electron Mass Ratio from Alcohol in the Early Universe”. Science 339 (6115): 46–48.Bibcode:2013Sci…339…46B. doi:10.1126/science.1224898.
- Jump up^ Podolsky, Dmitry. “Top ten open problems in physics”. NEQNET. Archivedfrom the original on 22 October 2012. Retrieved 24 January 2013.
- ^ Jump up to:a b c d e Brooks, Michael (March 19, 2005). “13 Things That Do Not Make Sense”. New Scientist. Issue 2491. Retrieved March 7, 2011.
- Jump up^ Steinhardt, P. and Turok, N. (2006). “Why the Cosmological constant is so small and positive”. Science 312: 1180–1183. arXiv:astro-ph/0605173.Bibcode:2006Sci…312.1180S. doi:10.1126/science.1126231.
- Jump up^ Alan Sokal (July 22, 1996). “Don’t Pull the String Yet on Superstring Theory”.New York Times
- Jump up^ Joshi, Pankaj S. (January 2009). “Do Naked Singularities Break the Rules of Physics?”. Scientific American
- Jump up^ Dirac, Paul, “Quantised Singularities in the Electromagnetic Field“.Proceedings of the Royal Society A 133, 60 (1931).
- Jump up^ Li, Tianjun; Dimitri V. Nanopoulos; Joel W. Walker (2011). “Elements of F-ast Proton Decay”. Nuclear Physics B 846: 43–99. arXiv:1003.2570.Bibcode:2011NuPhB.846…43L. doi:10.1016/j.nuclphysb.2010.12.014.
- Jump up^ Hansson, Johan (2010). “The “Proton Spin Crisis” — a Quantum Query” (PDF).Progress in Physics 3. Retrieved 14 April 2012.
- Jump up^ A. Blumhofer, M. Hutter (1997). “Family Structure from Periodic Solutions of an Improved Gap Equation”. Nuclear Physics B484: 80–96.Bibcode:1997NuPhB.484…80B. doi:10.1016/S0550-3213(96)00644-X.
- Jump up^ “India-based Neutrino Observatory (INO)”. Tata Institute of Fundamental Research. Retrieved 14 April 2012.
- Jump up^ Smarandache, Vic; Florentin Smarandache (2007). “Thirty Unsolved Problems in the Physics of Elementary Particles” (PDF). Progress in Physics 4.Bibcode:2009APS..HAW.KD010C.
- Jump up^ Nakamura (Particle Data Group), K; et al. (2010). “2011 Review of Particle Physics”. J. Phys. G 37 (7A): 075021. Bibcode:2010JPhG…37g5021N.doi:10.1088/0954-3899/37/7A/075021.
- Jump up^ Thomas Blum; Achim Denig; Ivan Logashenko; Eduardo de Rafael; Lee Roberts, B.; Thomas Teubner; Graziano Venanzoni (2013). “The Muon (g-2) Theory Value: Present and Future”. arXiv:1311.2198 [hep-ph].
- Jump up^ H. Muir (2 July 2003). “Pentaquark discovery confounds sceptics”. New Scientist. Retrieved 2010-01-08.
- Jump up^ G. Amit (14 July 2015). “Pentaquark discovery at LHC shows long-sought new form of matter”. New Scientist. Retrieved 2015-07-14.
- Jump up^ Laing, R. A.; Bridle, A. H. (2013). “Systematic properties of decelerating relativistic jets in low-luminosity radio galaxies”. arXiv:1311.1015 [astro-ph.CO].
- Jump up^ Strohmayer, Tod E.; Mushotzky, Richard F. (20 March 2003). “Discovery of X-Ray Quasi-periodic Oscillations from an Ultraluminous X-Ray Source in M82: Evidence against Beaming”. The Astrophysical Journal 586 (1): L61–L64. arXiv:astro-ph/0303665. Bibcode:2003ApJ…586L..61S. doi:10.1086/374732.
- Jump up^ Titarchuk, Lev; Fiorito, Ralph (10 September 2004). “Spectral Index and Quasi‐Periodic Oscillation Frequency Correlation in Black Hole Sources: Observational Evidence of Two Phases and Phase Transition in Black Holes” (PDF). The Astrophysical Journal 612 (2): 988–999. arXiv:astro-ph/0405360.Bibcode:2004ApJ…612..988T. doi:10.1086/422573. Retrieved 25 January2013.
- Jump up^ Shoji Kato (2012). “An Attempt to Describe Frequency Correlations among kHz QPOs and HBOs by Two-Armed Nearly Vertical Oscillations”. arXiv:1202.0121[astro-ph.HE].
- Jump up^ Ferrarese, Laura; Merritt, David (2000). “A Fundamental Relation between Supermassive Black Holes and their Host Galaxies”. The Astrophysical Journal 539: L9–L12. arXiv:astro-ph/0006053. Bibcode:2000ApJ…539L…9F.doi:10.1086/312838
- Jump up^ “Scientists Find That Saturn’s Rotation Period is a Puzzle”. NASA. June 28, 2004. Retrieved 2007-03-22.
- Jump up^ J J Condon, W D Cotton, E W Greisen, Q F Yin, R. A. Perley, G. B. Taylor, and J J Broderick.”The NRAO VLA Sky Survey”AJ, 115(5):1693-1716, May 1998.
- Jump up^ A. K. Singal. “Large Peculiar Motion of the Solar System from the Dipole Anisotropy in Sky Brightness due to Distant Radio Sources.”ApJL, 742:L23, December 2011.
- Jump up^ Prabhakar Tiwari, Rahul Kothari, Abhishek Naskar, Sharvari Nadkarni-Ghosh, Pankaj Jain. “Dipole anisotropy in sky brightness and source count distribution in radio NVSS data”.
- Jump up^ Prabhakar Tiwari and Pankaj Jain. “Dipole anisotropy in integrated linearly polarized flux density in NVSS data”.
- Jump up^ D. Hutsemékers “Evidence for very large-scale coherent orientations of quasar polarization vectors”A&A, 332:410-428, 1998.
- Jump up^ D. Hutsemékers and H. Lamy”Confirmation of the existence of coherent orientations of quasar polarization vectors on cosmological scales” A&A, 367(2):381-387, 2001.
- Jump up^ Pankaj Jain, Gaurav Narain, and S Sarala. “Large-scale alignment of optical polarizations from distant QSOs using coordinate-invariant statistics.”MNRAS, 347(2):394-402, 2004.
- Jump up^ Angélica de Oliveira-Costa, Max Tegmark, Matias Zaldarriaga, and Andrew Hamilton (2004). Significance of the largest scale cmb fluctuations in wmap. PhRvD, 69:063516.
- Jump up^ H.K. Eriksen, F.K. Hansen, A.J. Banday, K.M. Gorski, and P.B. Lilje. “Asymmetries in the Cosmic Microwave Background anisotropy field.”ApJ, 605:14–20, 2004.
- Jump up^ Pramoda Kumar Samal, Rajib Saha, Pankaj Jain, and John P. Ralston. “Testing Isotropy of Cosmic Microwave Background Radiation.”MNRAS, 385:1718, 2008.
- Jump up^ Pramoda Kumar Samal, Rajib Saha, Pankaj Jain, and John P. Ralston.”Signals of Statistical Anisotropy in WMAP Foreground-Cleaned Maps.”MNRAS, 396:511, 2009.
- Jump up^ Casagrande, L., et al. (2011) “New constraints on the chemical evolution of the solar neighbourhood and Galactic disc(s)“. Astronomy & Astrophysics, 2011, Volume 530, 138, 21 pp
- Jump up^ Bensby, T.; Feltzing, S.; Lundström, I. (July 2004). “A possible age-metallicity relation in the Galactic thick disk?”. Astronomy and Astrophysics 421 (3): 969–976.arXiv:astro-ph/0403591. Bibcode:2004A&A…421..969B. doi:10.1051/0004-6361:20035957.
- Jump up^ Gilmore, G.; Asiri, H.M. (00/2011). “Open Issues in the Evolution of the Galactic Disks“. Workshop on Gaia. Proceedings. Granada, ed. Navarro et al. 2011. Retrieved 2013-09-08.
- Jump up^ Casagrande, L., et al. (2016) “Measuring the vertical age structure of the Galactic disc using asteroseismology and SAGA“. MNRA, 2016, Volume 455, 987
- Jump up^ Brian D. Fields, The Primordial Lithium Problem
- Jump up^ André Balogh; Rudolf A. Treumann. “Physics of Collisionless Shocks: Space Plasma Shock Waves”. 2013. Section 7.4 “The Injection Problem”. p. 362.
- Jump up^ Futurism.com: “Tentatively finding even the most faint sign of extraterrestrial life would be the single most important discovery in the history of mankind, it could possibly help us find answers to the most existential mysteries of science(…)”
- Jump up^ F. Wagner (2007). “A quarter-century of H-mode studies”. Plasma Physics and Controlled Fusion 49: B1. Bibcode:2007PPCF…49….1W. doi:10.1088/0741-3335/49/12B/S01..
- Jump up^ Kenneth Chang (July 29, 2008). “The Nature of Glass Remains Anything but Clear”. The New York Times
- Jump up^ P.W. Anderson (1995). “Through the Glass Lightly”. Science 267 (5204): 1615.doi:10.1126/science.267.5204.1615-e.
The deepest and most interesting unsolved problem in solid state theory is probably the theory of the nature of glass and the glass transition.
- Jump up^ Cryogenic electron emission phenomenon has no known physics explanation. Physorg.com. Retrieved on 2011-10-20.
- Jump up^ Meyer, H. O. (1 March 2010). “Spontaneous electron emission from a cold surface”. EPL (Europhysics Letters) 89 (5): 58001. doi:10.1209/0295-5075/89/58001.
- Jump up^ Storey, B. D.; Szeri, A. J. (8 July 2000). “Water vapour, sonoluminescence and sonochemistry”. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 456 (1999): 1685–1709. doi:10.1098/rspa.2000.0582.
- Jump up^ Wu, C. C.; Roberts, P. H. (9 May 1994). “A Model of Sonoluminescence”.Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 445 (1924): 323–349. doi:10.1098/rspa.1994.0064.
- Jump up^ Goldstein, Melvyn L. (2001). “Major Unsolved Problems in Space Plasma Physics”. Astrophysics and Space Science 277 (1/2): 349–369.Bibcode:2001Ap&SS.277..349G. doi:10.1023/A:1012264131485.
- Jump up^ Yoshida, Beni (2011). “Feasibility of self-correcting quantum memory and thermal stability of topological order”. Annals of Physics 326 (10): 2566.arXiv:1103.1885. Bibcode:2011AnPhy.326.2566Y.doi:10.1016/j.aop.2011.06.001. Retrieved 8 April 2012.
- Jump up^ Schlein, Benjamin. “Graduate Seminar on Partial Differential Equations in the Sciences – Energy and Dynamics of Boson Systems”. Hausdorff Center for Mathematics. Retrieved 23 April 2012.
- Jump up^ Mukherjee, Prabir K. (1998). “Landau Theory of Nematic-Smectic-A Transition in a Liquid Crystal Mixture”. Molecular Crystals & Liquid Crystals 312: 157–164.doi:10.1080/10587259808042438. Retrieved 28 April 2012.
- Jump up^ A. Yethiraj, “Recent Experimental Developments at the Nematic to Smectic-A Liquid Crystal Phase Transition”, Thermotropic Liquid Crystals: Recent Advances, ed. A. Ramamoorthy, Springer 2007, chapter 8.
- Jump up^ Norris, David J. (2003). “The Problem Swept Under the Rug”. In Klimov, Victor.Electronic Structure in Semiconductors Nanocrystals: Optical Experiment (inSemiconductor and Metal Nanocrystals: Synthesis and Electronic and Optical Properties). CRC Press. p. 97. ISBN 9780203913260.
- Jump up^ Castelvecchi, Davide; Witze, Witze (February 11, 2016). “Einstein’s gravitational waves found at last”. Nature News. doi:10.1038/nature.2016.19361. Retrieved2016-02-11.
- Jump up^ B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016).“Observation of Gravitational Waves from a Binary Black Hole Merger”. Physical Review Letters 116 (6). doi:10.1103/PhysRevLett.116.061102.
- Jump up^ “Gravitational waves detected 100 years after Einstein’s prediction | NSF – National Science Foundation”. http://www.nsf.gov. Retrieved 2016-02-11.
- Jump up^ Philip M. Pearle (1970), “Hidden-Variable Example Based upon Data Rejection”,Phys. Rev. D 2 (8): 1418–25, doi:10.1103/PhysRevD.2.1418
- Jump up^ Hensen, B.; et al. (21 October 2015). “Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres”. Nature 526: 682–686.doi:10.1038/nature15759. Retrieved 21 October 2015.
- Jump up^ Markoff, Jack (21 October 2015). “Sorry, Einstein. Quantum Study Suggests ‘Spooky Action’ Is Real.”. New York Times. Retrieved 21 October 2015.
- Jump up^ Giustina, M.; et al. (16 December 2015). “Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons”. Physical Review Letters 115: 250401.doi:10.1103/PhysRevLett.115.250401.
- Jump up^ Shalm, L. K.; et al. (16 December 2015). “Strong Loophole-Free Test of Local Realism”. Physical Review Letters 115: 250402.doi:10.1103/PhysRevLett.115.250402.
- Jump up^ R. Aaij et al. (LHCb collaboration) (2015). “Observation of J/ψp resonances consistent with pentaquark states in Λ0
b→J/ψK−
p decays”. Physical Review Letters115 (7). arXiv:1507.03414. Bibcode:2015PhRvL.115g2001A.doi:10.1103/PhysRevLett.115.072001. - Jump up^ Khaire and Srianand 2015, [1], MNRAS Letters,
- Jump up^ http://www.devonhistorysociety.org.uk/2009/10/widecombe-great-storm-1638.html
- Jump up^ Cen, Jianyong; Yuan, Ping; Xue, Simin (17 January 2014). “Observation of the Optical and Spectral Characteristics of Ball Lightning”. Physical Review Letters(American Physical Society) 112 (35001). Bibcode:2014PhRvL.112c5001C.doi:10.1103/PhysRevLett.112.035001. Retrieved 19 January 2014.
- ^ Jump up to:a b Ball, Philip (17 January 2014). “Focus: First Spectrum of Ball Lightning”.Focus (American Physical Society). Bibcode:2014PhyOJ…7….5B.doi:10.1103/Physics.7.5. Retrieved 19 January 2014.
- Jump up^ Higgs, Peter (2010-11-24). “My Life as a Boson” (PDF). Talk given by Peter Higgs at Kings College, London, Nov 24 2010, expanding on a paper originally presented in 2001. Retrieved 17 January 2013. – the original 2001 paper can be found at: Duff and Liu, ed. (2003) [year of publication]. 2001 A Spacetime Odyssey: Proceedings of the Inaugural Conference of the Michigan Center for Theoretical Physics, Michigan, USA, 21–25 May 2001. World Scientific. pp. 86–88. ISBN 9812382313. Retrieved 17 January 2013.
- Jump up^ http://adsabs.harvard.edu/full/1999A%26A…341L..71V
- Jump up^ Charles Francis; Erik Anderson (2012). “XHIP-II: Clusters and associations”.arXiv:1203.4945 [astro-ph.GA].
- Jump up^ OPERA collaboration (July 12, 2012). “Measurement of the neutrino velocity with the OPERA detector in the CNGS beam”. arXiv:1109.4897 [hep-ex].
- Jump up^ Turyshev, S.; Toth, V.; Kinsella, G.; Lee, S. C.; Lok, S.; Ellis, J. (2012). “Support for the Thermal Origin of the Pioneer Anomaly”. Physical Review Letters 108 (24): 241101. arXiv:1204.2507. Bibcode:2012PhRvL.108x1101T.doi:10.1103/PhysRevLett.108.241101. PMID 23004253.
- Jump up^ Overbye, Dennis (23 July 2012). “Mystery Tug on Spacecraft Is Einstein’s ‘I Told You So’”. The New York Times. Retrieved 24 January 2014.
- Jump up^ C. Kouveliotou et al. Identification of two classes of gamma-ray bursts. Astrophys.J., 413:L101–104, 1993.
- Jump up^ http://iopscience.iop.org/article/10.1086/305343/fulltext/
- Jump up^ http://www.lorentz.leidenuniv.nl/history/Einstein_archive/
- Jump up^ “The MKI and the discovery of Quasars”. Jodrell Bank Observatory. Retrieved2006-11-23.
- Jump up^ Hubble Surveys the “Homes” of Quasars Hubblesite News Archive, 1996-35
External links
- What don’t we know? Science journal special project for its 125th anniversary: top 25 questions and 100 more.
- List of links to unsolved problems in physics, prizes and research.
- Ideas Based On What We’d Like to Achieve
- 2004 SLAC Summer Institute: Nature’s Greatest Puzzles
- Dual Personality of Glass Explained at Last
- What we do and don’t know Review on current state of physics by Steven Weinberg, November 2013
- The crisis of big science Steven Weinberg, May 2012
- The 10 Biggest Unsolved Problems in Physics Johan Hansson, March 2015
Unsolved Problems in Statistics
There are many longstanding unsolved problems in mathematics for which a solution has still not yet been found. The unsolved problems in statistics are generally of a different flavor; according to John Tukey,[1] “difficulties in identifying problems have delayed statistics far more than difficulties in solving problems.” A list of “one or two open problems” (in fact 22 of them) was given by David Cox.[2]
Inference and testing
- How to detect and correct for systematic errors, especially in sciences where random errors are large (a situation Tukey termed uncomfortable science).
- The Graybill–Deal estimator is often used to estimate the common mean of two normal populations with unknown and possibly unequal variances. Though this estimator is generally unbiased, its admissibility remains to be shown.[3]
- Meta-analysis: Though independent p-values can be combined using Fisher’s method, techniques are still being developed to handle the case of dependent p-values.
- Behrens–Fisher problem: Yuri Linnik showed in 1966 that there is no uniformly most powerful test for the difference of two means when the variances are unknown and possibly unequal. That is, there is no exact test (meaning that, if the means are in fact equal, one that rejects the null hypothesis with probability exactly α) that is also the most powerful for all values of the variances (which are thus nuisance parameters). Though there are many approximate solutions (such as Welch’s t-test), the problem continues to attract attention[4] as one of the classic problems in statistics.
- Multiple comparisons: There are various ways to adjust p-values to compensate for the simultaneous or sequential testing of hypothesis. Of particular interest is how to simultaneously control the overall error rate, preserve statistical power, and incorporate the dependence between tests into the adjustment. These issues are especially relevant when the number of simultaneous tests can be very large, as is increasingly the case in the analysis of data from DNA microarrays.[citation needed]
- Bayesian statistics: A list of open problems in Bayesian statistics has been proposed.[5]
Experimental design
- As the theory of Latin squares is a cornerstone in the design of experiments, solving the problems in Latin squares could have immediate applicability to experimental design.
Problems of a more philosophical nature
- Sunrise problem: What is the probability that the sun will rise tomorrow?
- Sampling of species problem: How is a probability updated when there is unanticipated new data?[6]
- Doomsday argument: How valid is the probabilistic argument that claims to predict the future lifetime of the human race given only an estimate of the total number of humans born so far?
- Exchange paradox: Issues arise within the subjectivistic interpretation of probability theory; more specifically within Bayesian decision theory.[citation needed] This is still an open problem among the subjectivists as no consensus has been reached yet. Examples include:
- The two envelopes problem
- The necktie paradox
Notes
- Jump up^ Tukey, John W. (1954). “Unsolved Problems of Experimental Statistics”. Journal of the American Statistical Association (Journal of the American Statistical Association, Vol. 49, No. 268) 49 (268): 706–731. doi:10.2307/2281535. JSTOR 2281535.
- Jump up^ Cox, D.R. (1984) “Present position and potential developments: Some personal views — Design of experiments and regression”, Journal of the Royal Statistical Society, Series A, 147 (2), 306–315
- Jump up^ Nabendu Pal, Wooi K. Lim (1997) “A note on second-order admissibility of the Graybill–Deal estimator of a common mean of several normal populations”, Journal of Statistical Planning and Inference, 63 (1), 71–78. doi:10.1016/S0378-3758(96)00202-9
- Jump up^ Fraser, D.A.S.; Rousseau, J. (2008) “Studentization and deriving accurate p-values”. Biometrika, 95 (1), 1—16. doi:10.1093/biomet/asm093
- Jump up^ Jordan, M. I. (2011). “What are the open problems in Bayesian statistics?” The ISBA Bulletin, 18(1).
- Jump up^ Zabell, S. L. (1992). “Predicting the unpredictable”. Synthese 90: 205. doi:10.1007/bf00485351.
References
- Linnik, Jurii (1968). Statistical Problems with Nuisance Parameters. American Mathematical Society. ISBN 0-8218-1570-9.
- Sawilowsky, Shlomo S. (2002). “Fermat, Schubert, Einstein, and Behrens–Fisher: The Probable Difference Between Two Means When σ1 ≠ σ2“, Journal of Modern Applied Statistical Methods, 1(2).
We feel that even if all possible scientific questions be answered, the problems of life have still not been touched at all. But of course there is then no question left, and just this is the answer.
– Wittgenstein





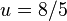 fractional quantum Hall state.
fractional quantum Hall state.